ベクトルの大きさを変える

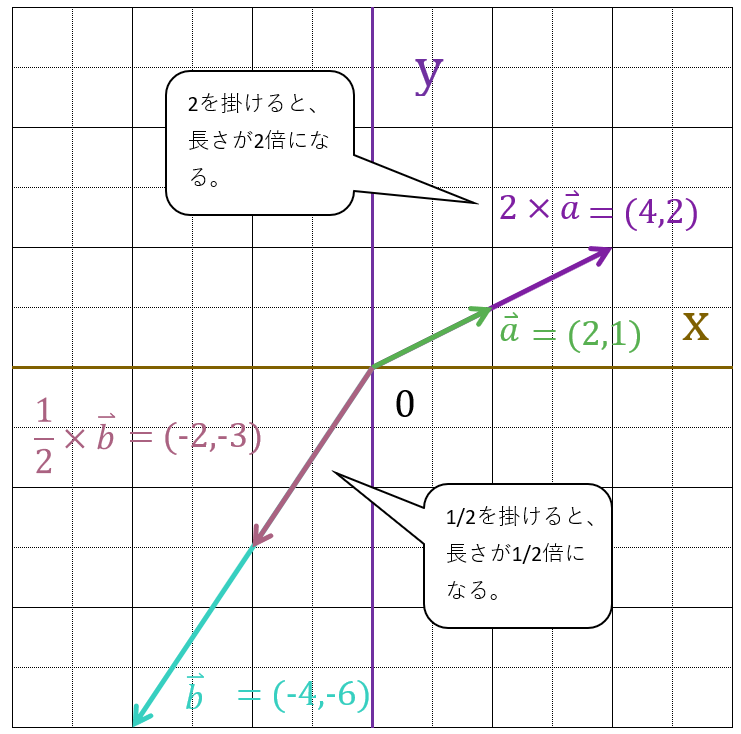
ベクトルは、スカラー値を掛けることで、大きさを変えることができます。

ベクトルの大きさを2倍にしたい場合は、スカラー値「2」を掛けることで2倍にできます。

逆に$\frac{1}{2}$倍したい場合は、スカラー値「$\frac{1}{2}$」を掛けることで、$\frac{1}{2}$倍にできます。

ベクトルがN倍になる証明

ベクトルにNを掛けて、そのあとに大きさを求めることで、大きさが元のベクトルのN倍になっていることを証明できます。

まず、元のベクトルを定義します。

$\vec{a} = (x, y)$

元ベクトルの大きさは以下になります。

$|\vec{a}| = \sqrt{x^2 + y^2}$

次にベクトルにスカラー値$N$を掛けます。

$N\times\vec{a} = (Nx, Ny)$

このNを掛けたベクトルの大きさを求めてみると・・・

$|N\times\vec{a}| = \sqrt{(Nx)^2 + (Ny)^2} = \sqrt{N^2 \times x^2 + N^2 \times y^2} = \sqrt{N^2 \times (x^2 + y^2)} = N \times \sqrt{x^2 + y^2}$

よって、$N$を掛けたベクトルの大きさは、

$N \times \sqrt{x^2 + y^2}$

になります。

元のベクトルと大きさを比較すると・・・

元の大きさ = $\sqrt{x^2 + y^2} $

Nを掛けた時の大きさ = $N \times \sqrt{x^2 + y^2}$

となり、Nを掛けたベクトルは、元のベクトルの大きさからN倍の大きさになっています。

コメントを残す コメントをキャンセル