ベクトルの正規化

ベクトルの大きさを1にすることを、ベクトルの正規化と言います。

ベクトルの大きさを１にするには、ベクトルをベクトルの大きさで割ることで、１にできます。

実際に $\vec{a} = (4,4)$ を正規化してみましょう。

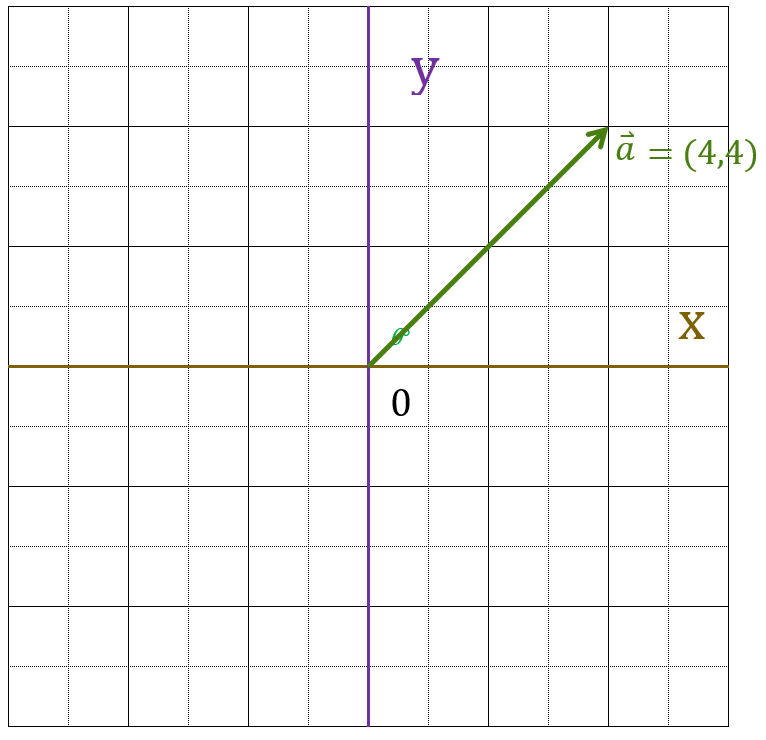
まずベクトルの大きさを求めます。

ベクトルの大きさを求めると

$\sqrt{4^2 + 4^2} = \sqrt{32} = 4\sqrt{2}$

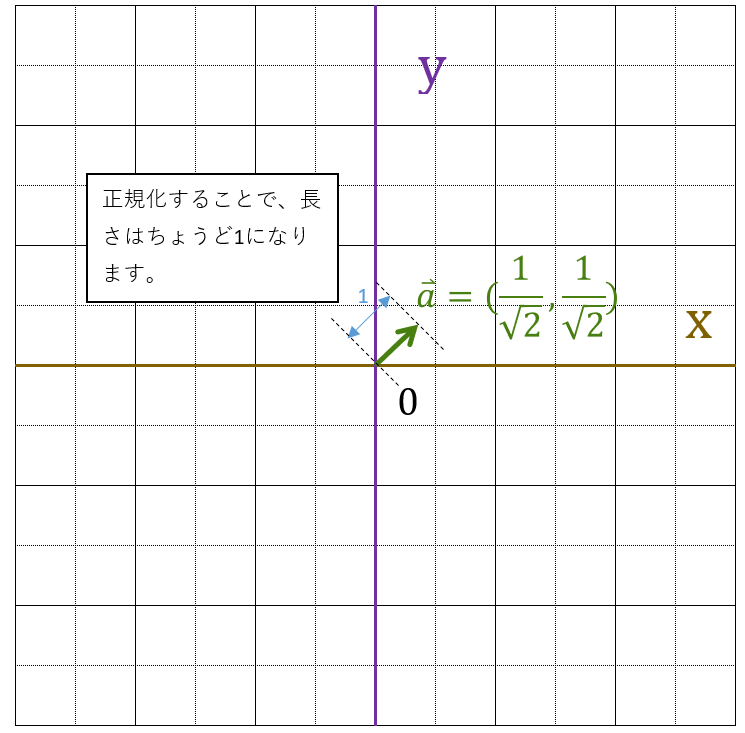
次にベクトルを求めた大きさで割ることで正規化が完了です。

$\frac{1}{4\sqrt{2}}\times\vec{a} = \frac{1}{4\sqrt{2}}\times(4,4) = (\frac{1}{4\sqrt{2}}\times 4, \frac{1}{4\sqrt{2}}\times4) = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})$

よって、 $(4,4)$ を正規化すると、 $(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})$ になります。

練習問題

(問) 以下のベクトルを正規化せよ。

①　$ \vec{a} = (3, 4) $

②　$ \vec{b} = (-2, 5) $

③　$ \vec{c} = (6, -8) $

④　$ \vec{d} = (1, 1) $

⑤　$ \vec{e} = (-7, -24) $

解答はこちら

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル