三角関数の加法定理とは以下になります。
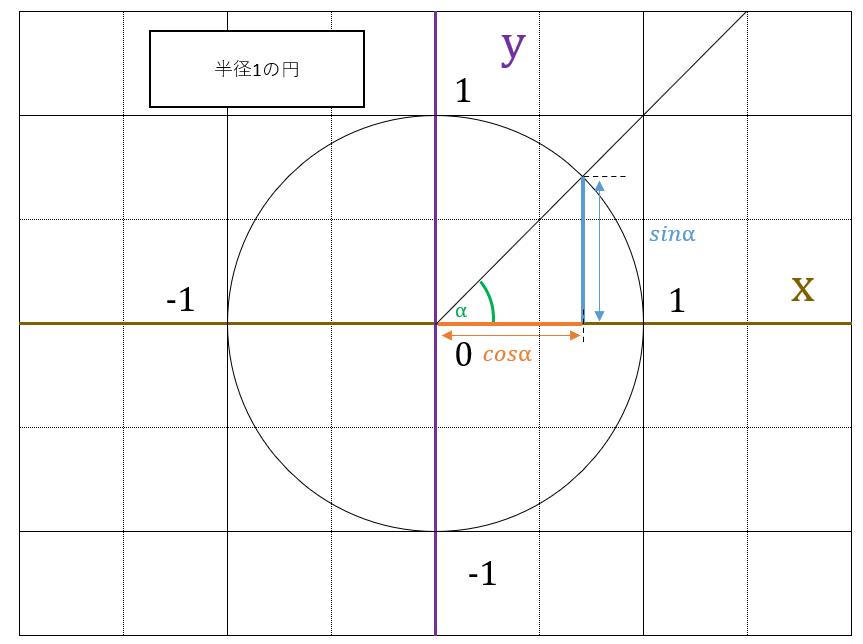
この三角関数の加法定理の証明は長くなりますので今は省略しますが、後々に証明も載せたいと思っています。
【Q.】この定理が何の役に立つの?
【A.】この三角関数の加法定理
いっけんすると何の役に立つのかよくわからない数式になっています。
実際、おそらく日常ではあまり役に立たないと思いますが、この三角関数の加法定理は、微分積分学等の様々な分野でも使用される非常に重要な定理です。
そして、何よりも、この三角関数の加法定理が、回転行列という技術の正体と言ってもいいものです。
今はまだ、どのように役立つのかよくわからない数式ですが、3D数学の心臓とも呼べる重要な定理ですので、しっかりと覚えましょう。
加法定理を使って、以下の練習問題を解いてみましょう
(1) 以下の式を三角関数の加法定理を用いて展開せよ。
$ \sin(18^\circ + 11^\circ) $
(2) 加法定理を使用して、以下の値を求めよ。
$ \sin30^\circ \cos15^\circ + \cos30^\circ \sin15^\circ $
(1)の解答
三角関数の加法定理の公式「」に当てはめるだけで完了です。
$\alpha = 18^\circ$、$\beta= 11^\circ$を代入すると・・・
$\sin(18^\circ + 11^\circ) = \sin18^\circ \cos11^\circ + \cos18^\circ \sin11^\circ$
これが答えになります。
(2)の解答
(2) の式は、すでに加法定理を使って展開した形になっています。
$ \sin30^\circ \cos15^\circ + \cos30^\circ \sin15^\circ $ を、加法定理を使って元の一つにまとまってる形に戻してやると・・・ $ \sin\alpha\cos\beta + \cos\alpha\sin\beta = \sin30^\circ \cos15^\circ + \cos30^\circ \sin15^\circ = \sin(30^\circ + 15^\circ) = \sin45^\circ $ となります。
$ \sin45^\circ $だとわかったので、後は三角関数の表を使って、$ \sin45^\circ $の値を求めれば完了です。
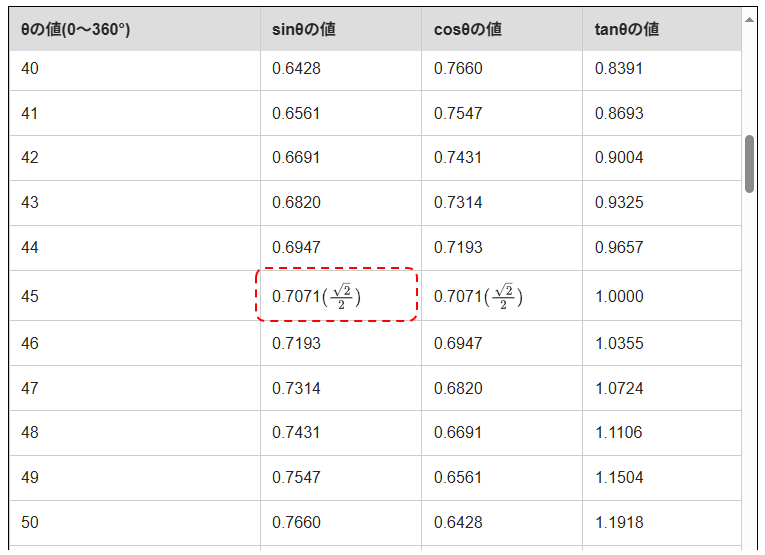
三角関数の表から$ \sin45^\circ $の値は$\dfrac{\sqrt{2}}{2}$です。
よって、答えは、$\dfrac{\sqrt{2}}{2} $ になります。
以下の式を三角関数の加法定理を用いて展開せよ。
① $ \sin(18^\circ + 30^\circ) $
② $ \sin(36^\circ + 45^\circ) $
③ $ \sin(60^\circ + 72^\circ) $
④ $ \cos(18^\circ + 30^\circ) $
⑤ $ \cos(36^\circ + 45^\circ) $
⑥ $ \cos(60^\circ + 72^\circ) $
加法定理を使用して、以下の値を求めよ。
① $ \sin30^\circ \cos15^\circ + \cos30^\circ \sin15^\circ $
② $ \cos45^\circ \cos45^\circ – \sin45^\circ \sin45^\circ $
③ $ \sin60^\circ \cos30^\circ + \cos60^\circ \sin30^\circ $
④ $ \sin18^\circ \cos30^\circ + \cos18^\circ \sin30^\circ $
⑤ $ \cos72^\circ \cos15^\circ – \sin72^\circ \sin15^\circ $
⑥ $ \sin18^\circ \cos36^\circ + \cos18^\circ \sin36^\circ $
