今回は複数の座標をまとめて回転する方法を学びます。
複数の座標をまとめて回転するには、以下の操作をします。
複数の座標をまとめて回転
(1)複数のベクトルを並べた行列を作る
(2)回転行列で回転を実行
(3)計算結果の行列をベクトルに戻す
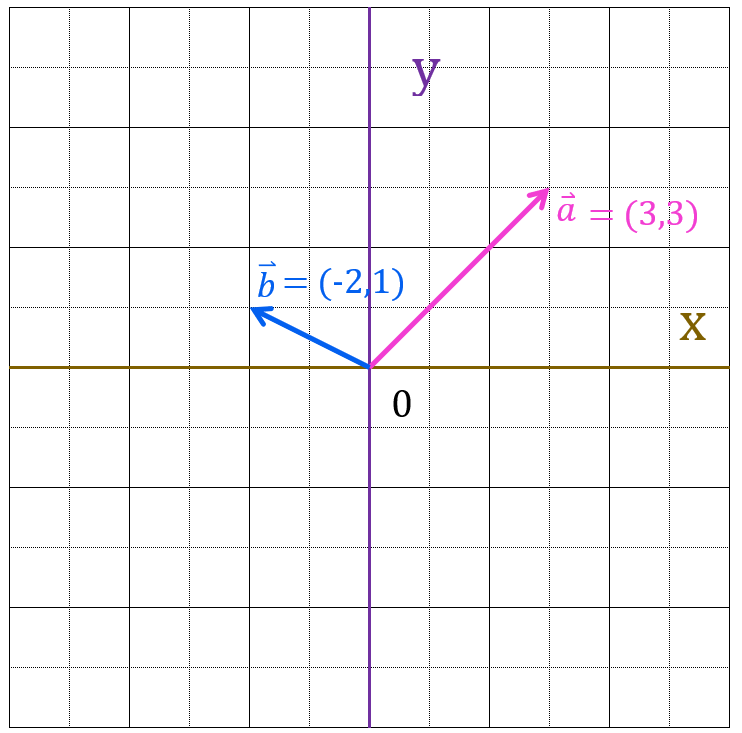
早速以下の2つのベクトルを30度回転してみましょう。
練習
(1)$\vec{a} = (3,\;3)$
(2)$\vec{b} = (-2,\;1)$
まず最初にベクトルを縦に並べた行列を作ります。
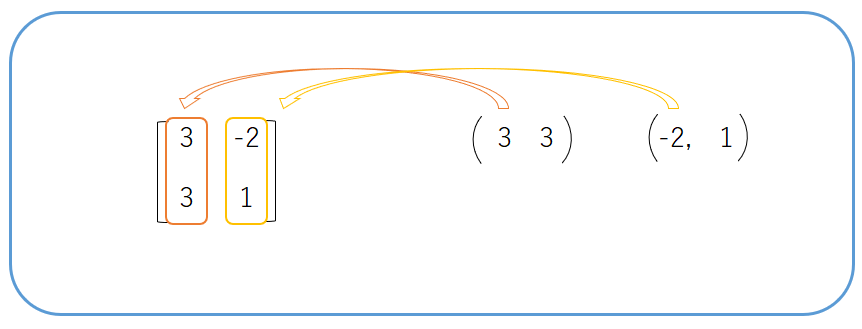
行列を作ったら回転行列を掛けて、回転を実行します。
$ \begin{bmatrix} \cos30^\circ & -\sin30^\circ \\ \sin30^\circ & \cos30^\circ \end{bmatrix} \times \begin{bmatrix} 3 & -2 \\ 3 & 1 \end{bmatrix} = \begin{bmatrix} 0.8660 & -0.5000 \\ 0.5000 & 0.8660 \end{bmatrix} \times \begin{bmatrix} 3 & -2 \\ 3 & 1 \end{bmatrix} = \begin{bmatrix} 1.0980 & -2.2320 \\ 4.0980 & -0.1340 \end{bmatrix} $最後に、計算結果の行列をベクトルに戻したら完了です。

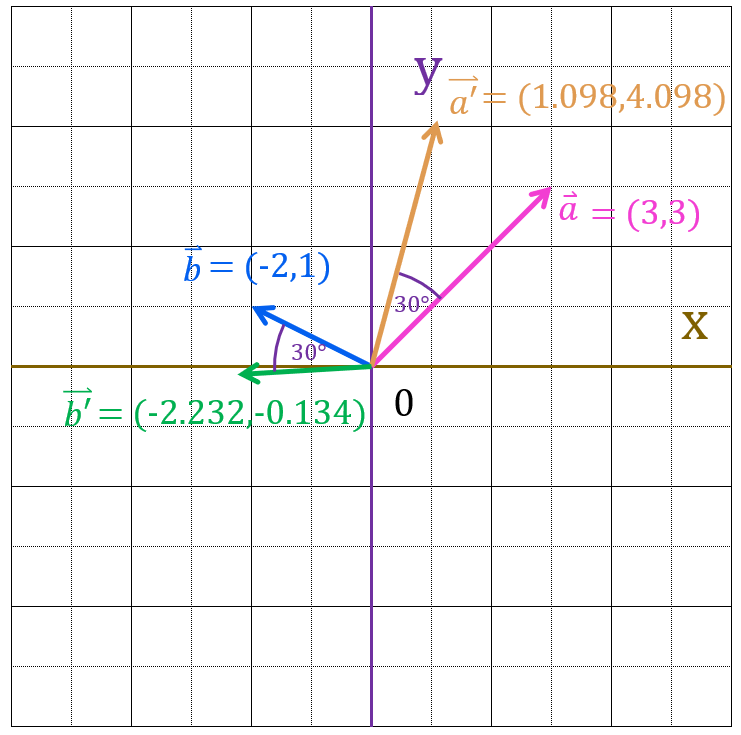
よって
$\vec{a} = (3,3)$を30度回転回転させると、$\vec{a’} = (1.0980, 4.0980)$
$\vec{b} = (-2,1)$を30度回転回転させると、$\vec{b’} = (-2.2320, -0.1340)$
になります。
お疲れ様でした。
これで、回転行列の章は終わりです。
次は、いよいよプログラミングです。
練習問題
以下の複数のベクトルを、回転行列を使用して指定の角度で回転せよ。
| ① $\vec{a} = (2,\ 2)$ | $\vec{b} = (3,\ -1)$ | 角度:30° | |
| ② $\vec{a} = (-1,\ 4)$ | $\vec{b} = (2,\ -3)$ | 角度:60° | |
| ③ $\vec{a} = (5,\ -2)$ | $\vec{b} = (-3,\ 1)$ | $\vec{c} = (1,\ 4)$ | 角度:120° |
