行列の掛け算の定義は以下になります。
行列 $A$ の列数と、行列 $B$ の行数が一致しているとき、掛け算が可能です。
また掛け算後の行列の形は、Aの行数とBの列数が新たな行列の形になります
行列の掛け算の定義(2×3 × 3×2の場合)
(2行3列)
(3行2列)
(2行2列)
早速以下の行列を一緒に計算してみましょう。
まずは1行2列の行列と2行1列の行列の掛け算をしてみます。
1行2列の行列と2行1列の行列の掛け算なので、掛け算後の行列の形は1行1列です。
練習

行列Aと行列Bを両方ベクトルとみなして内積を計算します。(内積のリンクはこちら)

11になりました。これで計算は完了です。
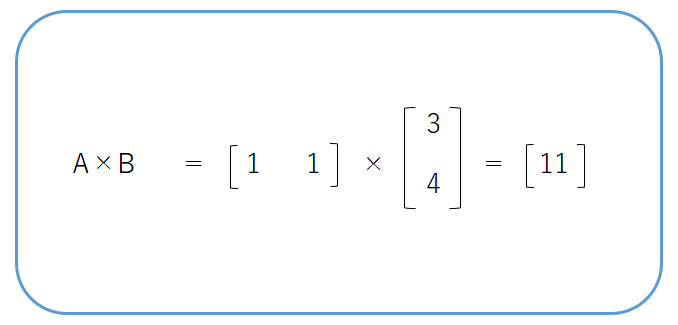
練習問題
以下の行列の積 $A \times B$ を計算せよ。
| (1) $A = \begin{bmatrix} 3 & -2 \end{bmatrix}$ | $B = \begin{bmatrix} 4 \\ 1 \end{bmatrix}$ |
| (2) $A = \begin{bmatrix} -1 & 5 \end{bmatrix}$ | $B = \begin{bmatrix} 2 \\ -3 \end{bmatrix}$ |
| (3) $A = \begin{bmatrix} 0 & 6 \end{bmatrix}$ | $B = \begin{bmatrix} -2 \\ 1 \end{bmatrix}$ |
| (4) $A = \begin{bmatrix} 7 & -4 \end{bmatrix}$ | $B = \begin{bmatrix} 1 \\ 5 \end{bmatrix}$ |
| (5) $A = \begin{bmatrix} -3 & -3 \end{bmatrix}$ | $B = \begin{bmatrix} -2 \\ -2 \end{bmatrix}$ |
