ベクトルの三角関数表示

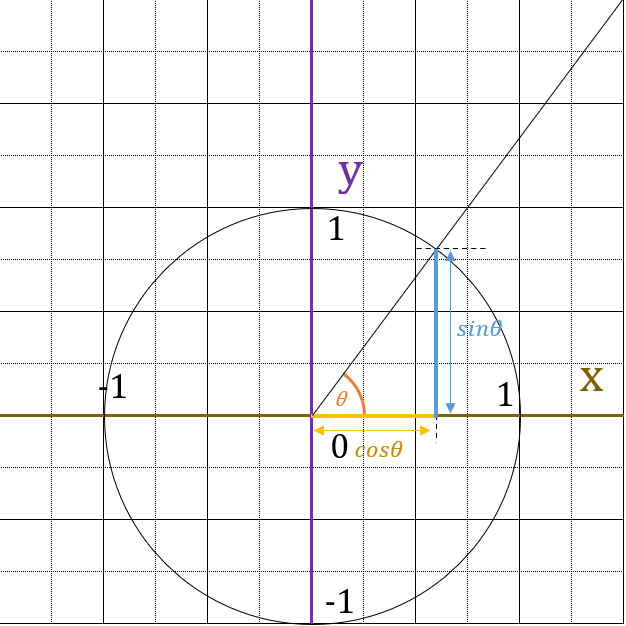
今回は、ベクトルの三角関数表示を解説します。

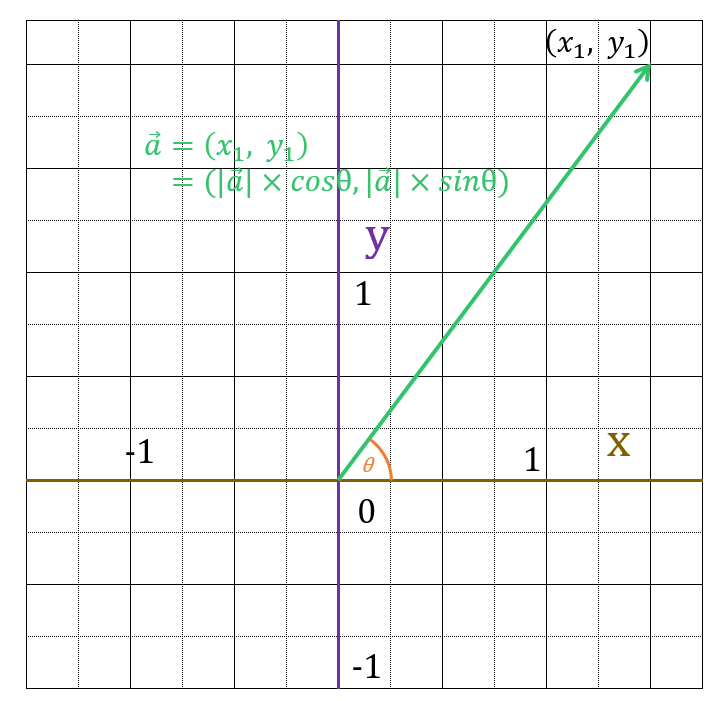
まず、ベクトル$\vec{a}=(x_1, \; y_1)$を正規化して、ベクトルの大きさを1にします。

正規化したベクトルを、$\vec{a’}=(x’_1, \; y’_1)$とします。

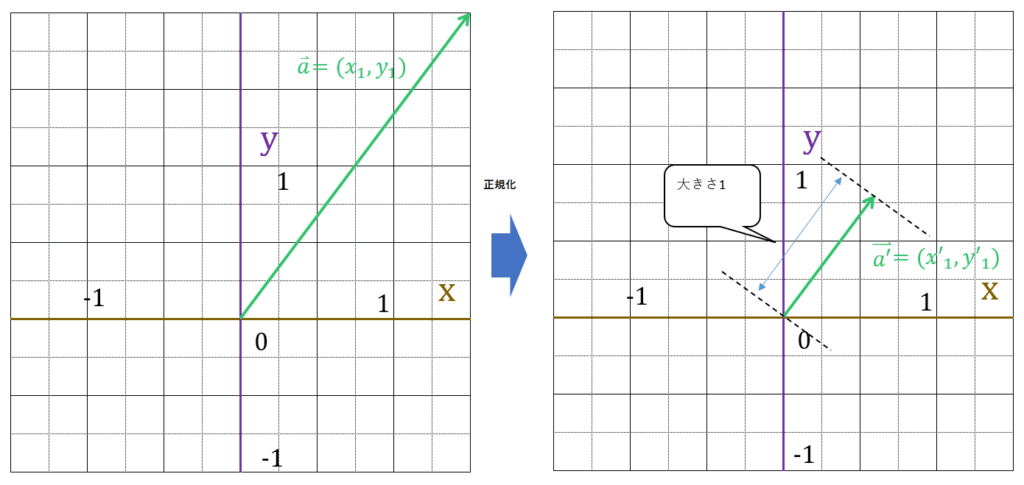
そして、正規化したベクトルの図に半径１の円を描きます。

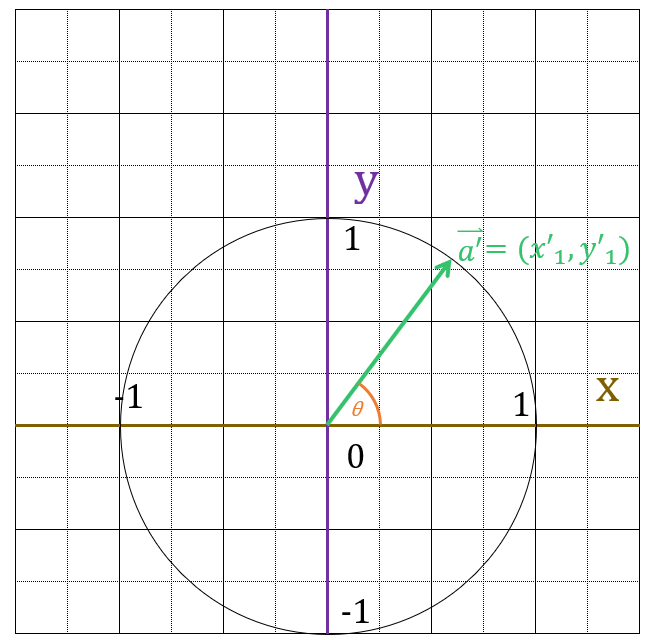
さらに、$x’_1$と$y’_1$の長さをこの図に描きます

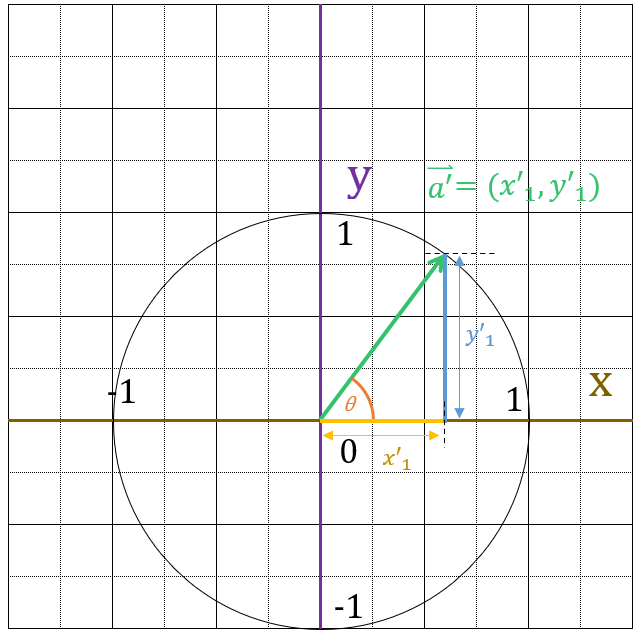
ここで$sin\theta,\; cos\theta$と比較します。

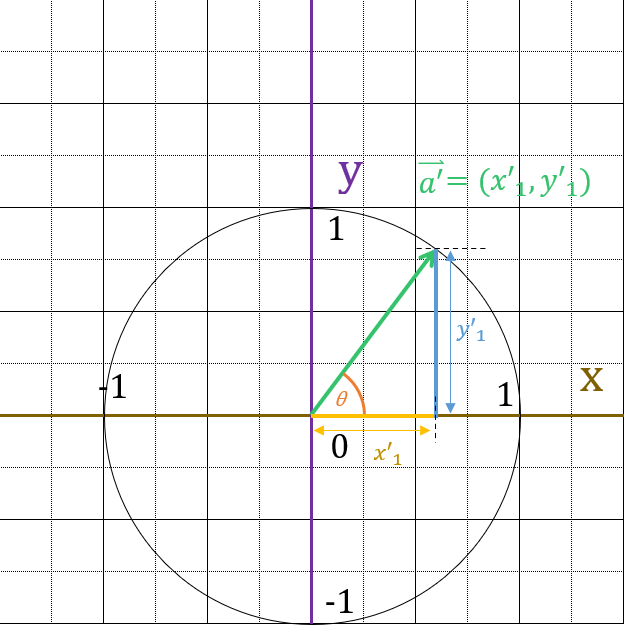
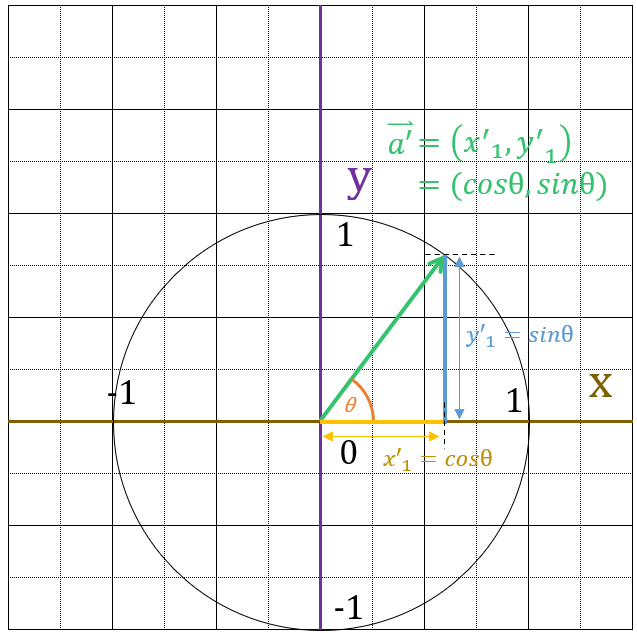
比較すると、$x’_1 = \cos\theta$、$y’_1 = \sin\theta$になっていることがわかります。

よって、$x$軸とベクトル$\vec{a}$のなす角度を$\theta$とし、ベクトル$\vec{a}$を正規化したベクトルを$\vec{a’} = (x’_1, \;y’_1)$とすると

$x’_1 = \cos\theta$、$y’_1 = \sin\theta$が成り立ちます。

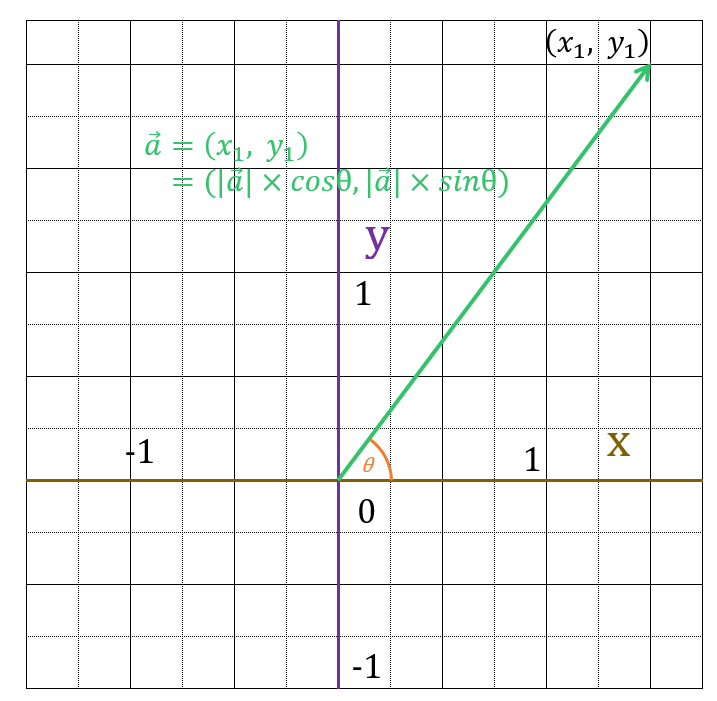
最後に$\vec{a’}$は正規化されているので、サイズが1になっています。そのため元の大きさを掛け算して、元のサイズに戻してやります。すると、元のベクトルに戻ります。よって

$|\vec{a}|\times \vec{a’} = (|\vec{a}|\times x’_1,\; |\vec{a}|\times y’_1) = (|\vec{a}|\times cos\theta,\; |\vec{a}|\times sin\theta) = \vec{a}$

が成り立ちます。

よって、$x$軸とベクトル$\vec{a}$のなす角度を、$\theta$とすると

が成り立ちます

証明終了

このベクトルの三角関数表示は、回転行列の原理を証明するときに必須です。しっかりと覚えておきましょう。