ベクトルの三角関数表示２

前回、ベクトルの三角関数表示を学習しましたが、今回は実際に、ベクトルを三角関数表示してみます。

早速、以下の練習問題を解きましょう。

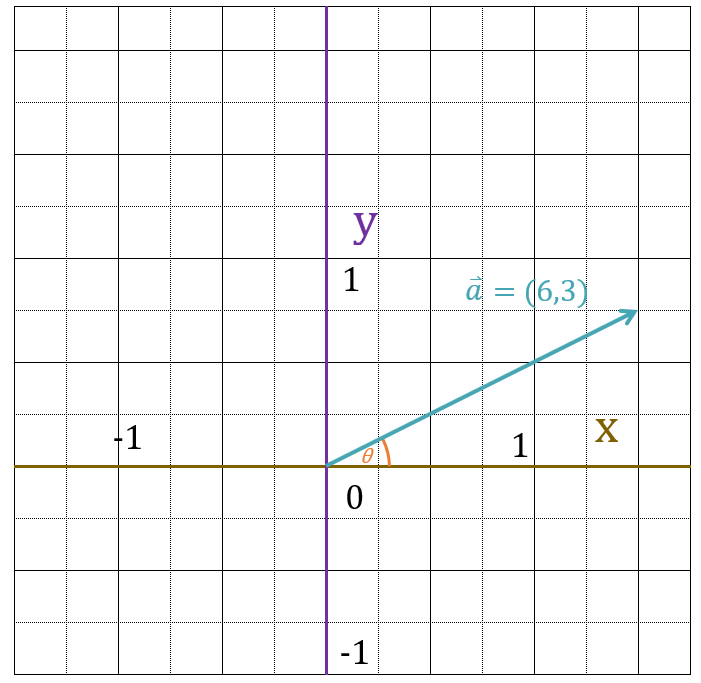
ベクトルを三角関数表示するには、ベクトルx軸のなす角度θを特定しなければなりません。

まず、ベクトルを正規化します。

まずベクトルの長さを求めます

$ |\vec{a}| = \sqrt{6^2 + 3^2} = \sqrt{36 + 9} = \sqrt{45} = 3\sqrt{5} $

次に各成分を長さで割って正規化完了です。

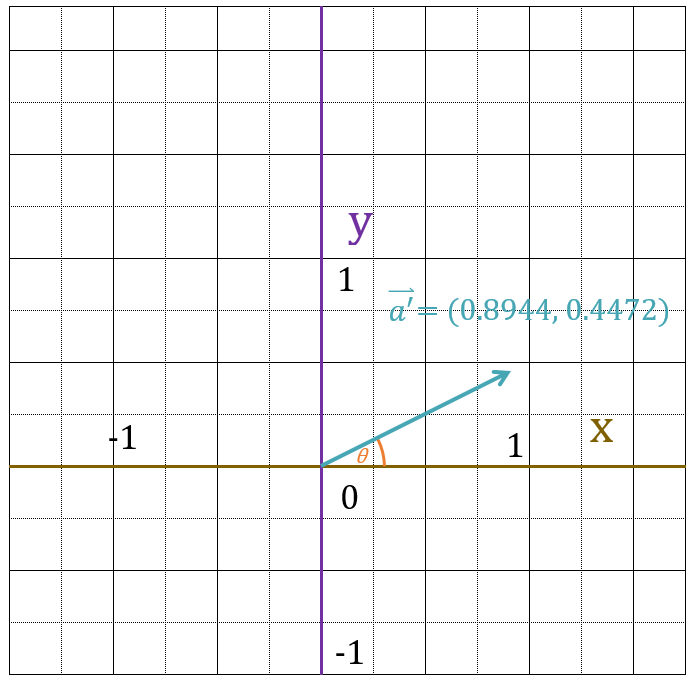
次に、ベクトルの三角関数表示より、$cos\theta = 0.8944$、$sin\theta = 0.4472$が成り立ちます。

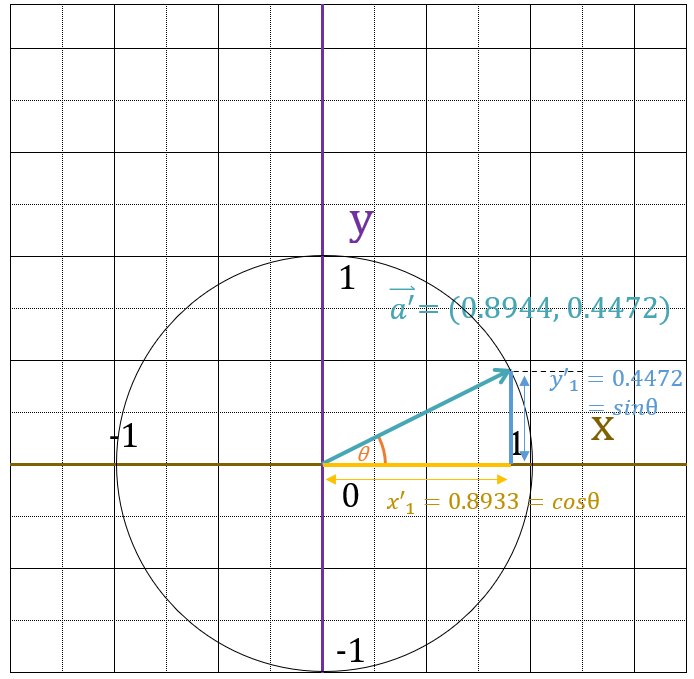
$cos\theta$と、$sin\theta$の値がわかったので、三角関数の表を使って角度θを特定します。

$sin\theta = 0.4472$、$cos\theta = 0.8944$と最も近い行を探すと・・・

27度です。よって、$\vec{a’} = (0.8944,\;0.4472) = (cos27^\circ,\;sin27^\circ)$が成り立ちます。

最後に、$\vec{a’} $は正規化されて大きさが１になってるので元の大きさに戻してやります。

$|\vec{a}| \times\vec{a’} = \vec{a} =  (3\sqrt{5}\cdot cos27^\circ,\;3\sqrt{5}\cdot sin27^\circ)$

よって、$\vec{a} = (6,  3)$を三角関数表示すると

$\vec{a} = (6,  3) =  (3\sqrt{5}\cdot cos27^\circ,\;3\sqrt{5}\cdot sin27^\circ)$になります。

解答はこちら