今回は、ベクトルの三角関数表示を利用したベクトルの回転を学びます。
回転行列の原理の証明にも使用する操作なので、しっかりと覚えましょう
まず、ベクトルの三角関数表示の式をよく見てみます。
ベクトルは以下の等式が成り立つ
$\theta$は、$x$軸とベクトル$\vec{a}$のなす角度である
この数式をよく見てみると、ただのx,yという座標だけを表している情報が、
大きさと、向き(角度)という2つの情報に分離していることがわかります。
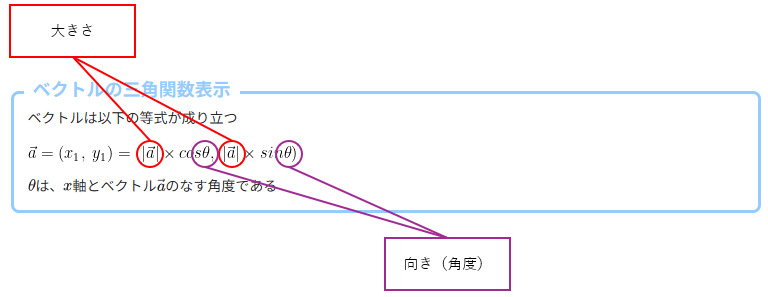
そのため、ベクトルを三角関数表示にした後に、向き(角度)だけを変えれば、大きさをそのままにして、ベクトルの回転を行えます。
早速、以下のベクトルを30度回転させてみましょう。
以下のベクトルを30度回転せよ
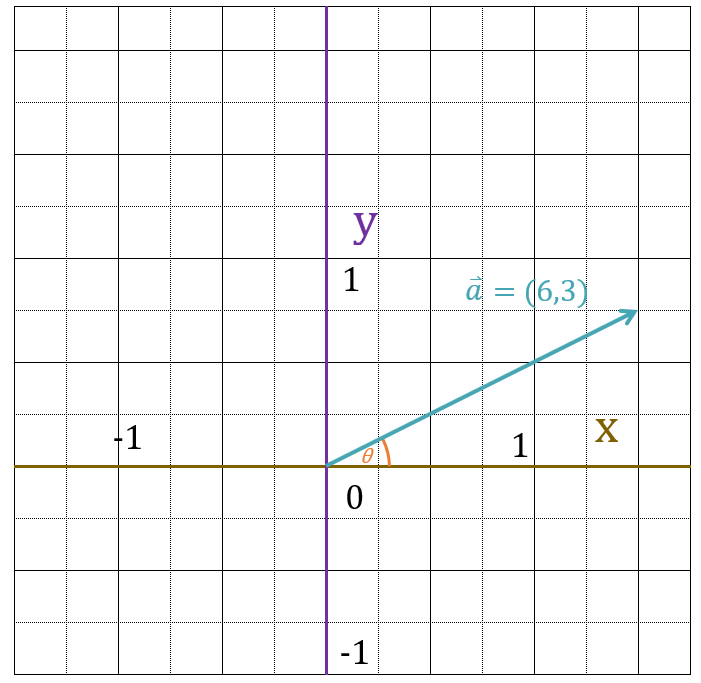
まず、ベクトルを三角関数表示に変換します。
ベクトルを三角関数表にすると、
$\vec{a} = (6, 3) = (3\sqrt{5}\cdot cos27^\circ,\;3\sqrt{5}\cdot sin27^\circ)$になります。
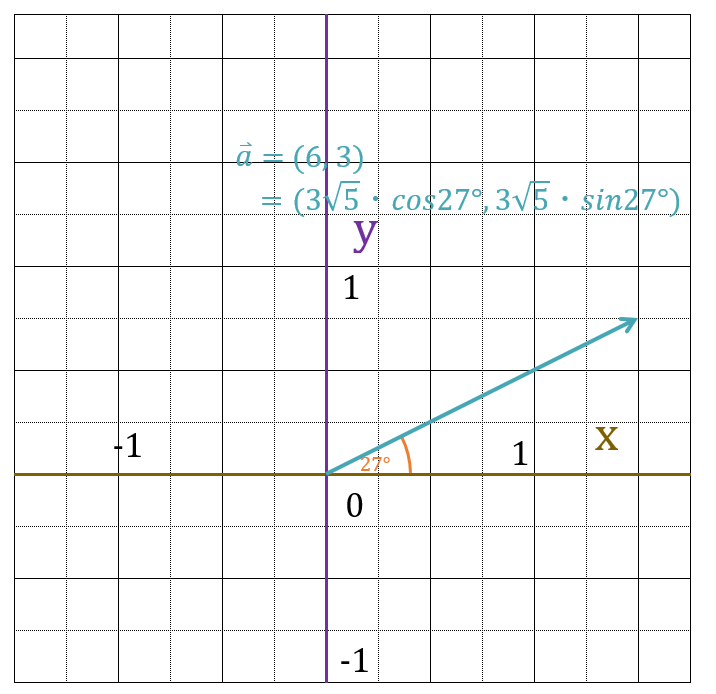
次に、27度に30度を足して57度にします。
そうすることで、ベクトルが30度回転します。
30度回転後のベクトルを$\vec{b}$とすると
$\vec{b} = (3\sqrt{5}\cdot cos57^\circ,\;3\sqrt{5}\cdot sin57^\circ)$になります。次に三角関数表示を元の座標に戻してやります。
$cos57^\circ,sin57^\circ$の値を三角関数表で求めると・・・
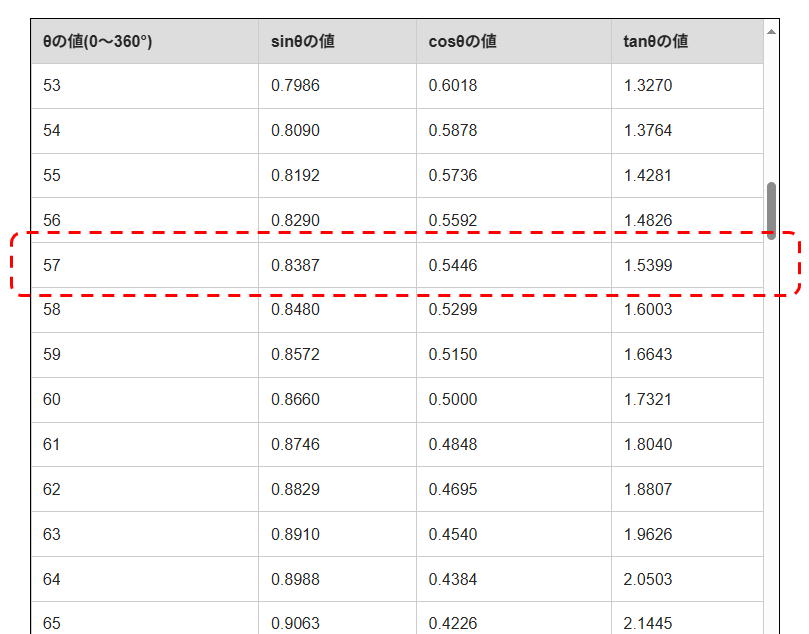
$cos57^\circ=0.5446,\;\;sin57^\circ=0.8387$になります。
よって、
$\vec{b} = (3\sqrt{5}\cdot cos57^\circ,\;3\sqrt{5}\cdot sin57^\circ) = (3\sqrt{5}\cdot 0.5446,\;3\sqrt{5}\cdot 0.8387) = (3.6557, 5.6267)$つまり、$\vec{a}$を30°回転させたベクトルを$\vec{b}$とすると
$\vec{b} = (3.6557, 5.6267)$になります。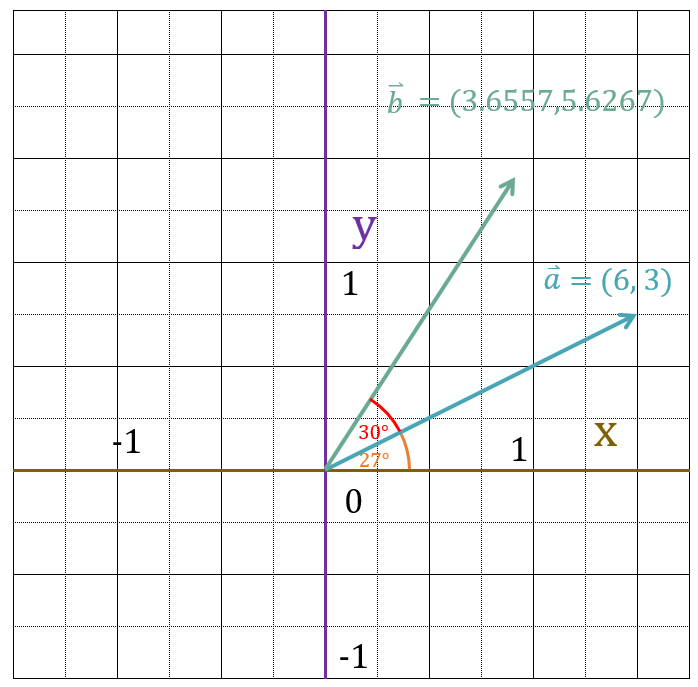
分度器で、角度を測ってみると、ベクトルがちゃんと30度回転しているのがわかります。
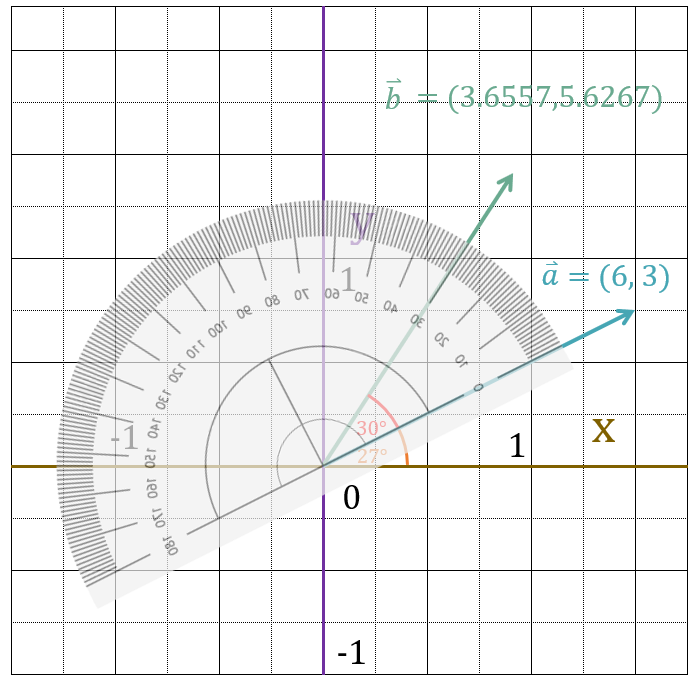
さらにベクトルの大きさの半径の円を描くと、ベクトルの大きさも変わっていないことがわかります。

以下のベクトルを以下の角度で回転せよ。
| ① $\vec{v} = (3,\ 4)$ | 角度:30° |
| ② $\vec{v} = (5,\ -2)$ | 角度:45° |
| ③ $\vec{v} = (-4,\ 1)$ | 角度:60° |
| ④ $\vec{v} = (2,\ -3)$ | 角度:90° |
| ⑤ $\vec{v} = (-6,\ -2)$ | 角度:120° |
