行列の足し算の定義は以下になります。
行列の足し算の定義
行列の足し算は同じ成分を足し合わせることで、求めることができます。
行列の足し算の具体例
しかし、行列の行数、もしくは列数が異なる場合は、足し算ができません。
足し算ができない行列の例を見てみましょう。
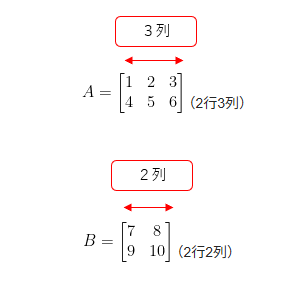
足し算ができない行列の例
(2行3列)
(2行2列)
この場合、行列 $A$ と $B$ は列数が異なるため、足し算ができません。
行列の足し算を行うには、行と列の数が完全に一致している必要があります。サイズが異なる行列同士では、対応する成分が存在しないため、足し算はできません。
