解答
1章 ベクトル
1.ベクトルとは?
2.ベクトルの足し算
① $(2 + 4,\ 3 + 1) = (6,\ 4)$
② $(-1 + 3,\ 5 + (-2)) = (2,\ 3)$
③ $(0 + 7,\ 0 + (-3)) = (7,\ -3)$
④ $(-4 + 2,\ -6 + 9) = (-2,\ 3)$
⑤ $(1.5 + 3.5,\ 2.5 + (-1.5)) = (5.0,\ 1.0)$
3.ベクトルの引き算
① $(5 – 3,\ 2 – 1) = (2,\ 1)$
② $(-2 – 1,\ 4 – (-3)) = (-3,\ 7)$
③ $(0 – 6,\ 0 – 7) = (-6,\ -7)$
④ $(3.5 – 1.5,\ -2.5 – 1.5) = (2.0,\ -4.0)$
⑤ $(-5 – (-2),\ -5 – (-3)) = (-3,\ -2)$
4.ベクトルにスカラー値を掛け算する
① $ 3 \times \vec{a} = (3 \times -2, 3 \times -1) = (-6, -3)$
② $ -2 \times \vec{b} = (-2 \times 4, -2 \times 0) = (-8, 0)$
③ $ 0.5 \times \vec{c} = (0.5 \times 1, 0.5 \times -5) = (0.5, -2.5)$
④ $ -1 \times \vec{d} = (-1 \times -3, -1 \times 2) = (3, -2)$
⑤ $ 4 \times \vec{e} = (4 \times 0, 4 \times 7) = (0, 28)$
5.ベクトルの始点を変更する
始点ベクトル$ \vec{a} = (3,2) $ を足すことで図を描けます。
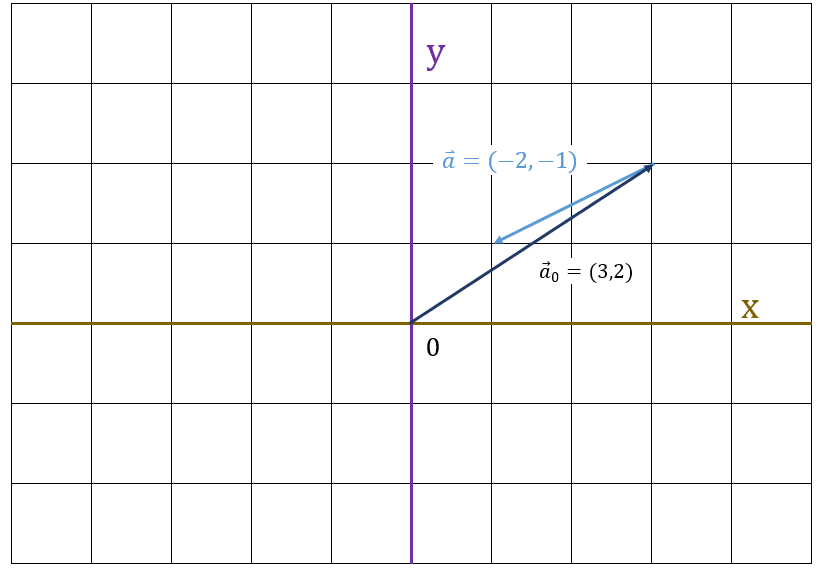
また、移動後の $ \vec{a} $ の座標を計算すると $ (1,1) $ になります。
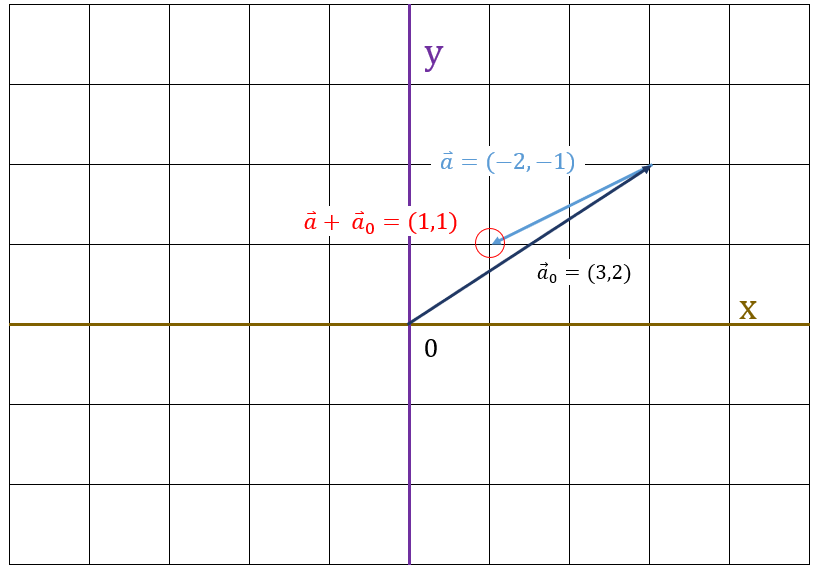
6.ピタゴラスの定理
7.ベクトルの大きさ
8.ベクトルの大きさを変える
9.ベクトルの正規化
① $ \vec{a} = (3, 4) $
$ |\vec{a}| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 $
正規化:$ \frac{1}{|\vec{a}|} \times \vec{a} = \frac{1}{5} \times (3, 4) = \left( \frac{3}{5}, \frac{4}{5} \right) $
② $ \vec{b} = (-2, 5) $
$ |\vec{b}| = \sqrt{(-2)^2 + 5^2} = \sqrt{4 + 25} = \sqrt{29} $
正規化:$ \frac{1}{\sqrt{29}} \times (-2, 5) = \left( \frac{-2}{\sqrt{29}}, \frac{5}{\sqrt{29}} \right) $
③ $ \vec{c} = (6, -8) $
$ |\vec{c}| = \sqrt{6^2 + (-8)^2} = \sqrt{36 + 64} = \sqrt{100} = 10 $
正規化:$ \frac{1}{10} \times (6, -8) = \left( \frac{6}{10}, \frac{-8}{10} \right) = (0.6, -0.8) $
④ $ \vec{d} = (1, 1) $
$ |\vec{d}| = \sqrt{1^2 + 1^2} = \sqrt{2} $
正規化:$ \frac{1}{\sqrt{2}} \times (1, 1) = \left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right) $
⑤ $ \vec{e} = (-7, -24) $
$ |\vec{e}| = \sqrt{(-7)^2 + (-24)^2} = \sqrt{49 + 576} = \sqrt{625} = 25 $
正規化:$ \frac{1}{25} \times (-7, -24) = \left( \frac{-7}{25}, \frac{-24}{25} \right) $
10.三角関数の復習
① $ \cos27^\circ = 0.8910 $
② $ \sin48^\circ = 0.7431 $
③ $ \tan63^\circ = 1.9626 $
④ $ \cos75^\circ = 0.2588 $
⑤ $ \sin15^\circ = 0.2588 $
11.ベクトルの内積
① $ \vec{a} = (3,3), \vec{b} = (4,0) $
成分の積:$ 3 \cdot 4 + 3 \cdot 0 = 12 $
大きさ×cosθ:$ \sqrt{18} \times 4 \times 0.7071 = 12.0000 $
② $ \vec{a} = (2,-1), \vec{b} = (-1,2) $
成分の積:$ 2 \cdot (-1) + (-1) \cdot 2 = -4 $
大きさ×cosθ:$ \sqrt{5} \times \sqrt{5} \times (-0.8000) = -4.0000 $
③ $ \vec{a} = (5,0), \vec{b} = (0,5) $
成分の積:$ 5 \cdot 0 + 0 \cdot 5 = 0 $
大きさ×cosθ:$ 5 \times 5 \times 0 = 0.0000 $
④ $ \vec{a} = (-3,4), \vec{b} = (6,8) $
成分の積:$ (-3) \cdot 6 + 4 \cdot 8 = 14 $
大きさ×cosθ:$ 5 \times 10 \times 0.2800 = 14.0000 $
⑤ $ \vec{a} = (1,2), \vec{b} = (2,1) $
成分の積:$ 1 \cdot 2 + 2 \cdot 1 = 4 $
大きさ×cosθ:$ \sqrt{5} \times \sqrt{5} \times 0.8000 = 4.0000 $
12.2つのベクトルのなす角度を求める
