前回は1行2列 × 2行1列の場合の計算を行いましたが、今回は2行2列の行列の掛け算をしてみます。
数式で表すと以下の式になります。
$ A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} $(2行2列)
$ B = \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} $(2行2列)
$ AB = \begin{bmatrix}
a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{12} + a_{12}b_{22} \\
a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{22}b_{22}
\end{bmatrix} $(2行2列)
早速以下の行列を一緒に計算してみましょう
2行2列の行列と2行2列の行列の掛け算なので、掛け算後の行列の形は2行2列です。
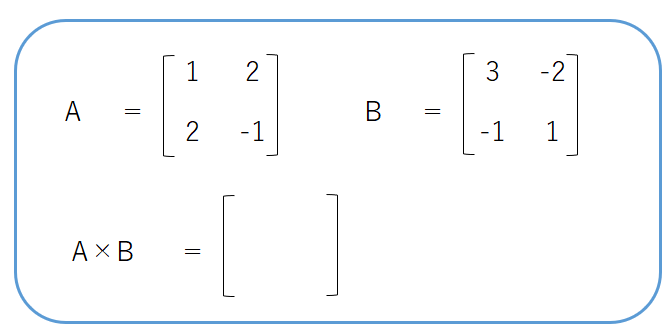
まずは、行列Aの1行目と、行列Bの1列目に対して、内積の計算を行います。
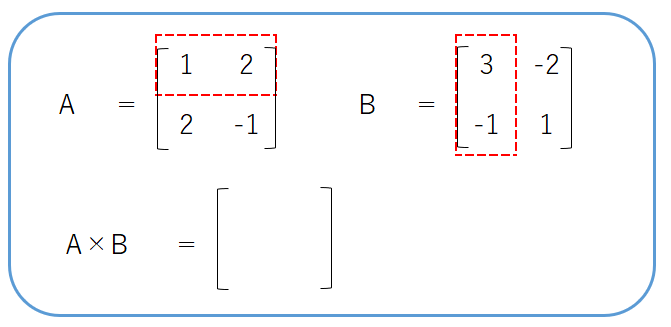
内積を計算すると、$ 1×3 + 2×(-1) = 3 – 2 = 1 $になったので、この値を$A×B$の1行目1列に代入します。
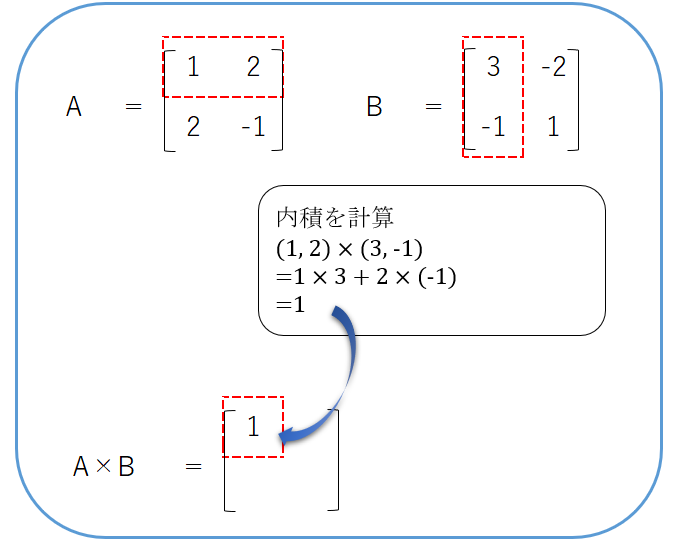
次に、行列Aの2行目と、行列Bの1列目に対して、内積の計算を行います。
内積を計算すると、$ 2×3 + (-1)×(-1) = 7 $になったので、この値を$A×B$の2行1列目に代入します。
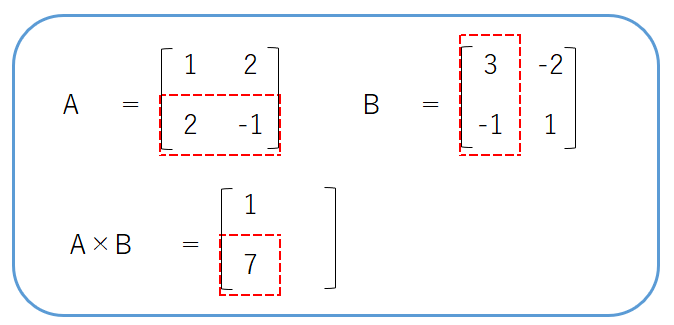
次に、行列Aの1行目と、行列Bの2列目に対して、内積の計算を行います。
内積を計算すると、$ 1×(-2) + 2×1 = 0 $になったので、この値を$A×B$の1行2列目に代入します。
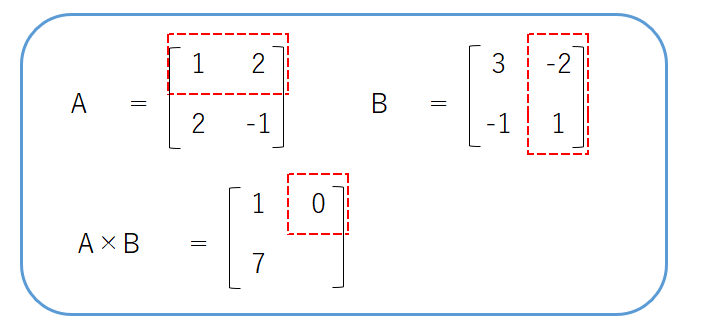
次に、行列Aの2行目と、行列Bの2列目に対して、内積の計算を行います。
内積を計算すると、$ 2×(-2) + (-1)×1 = -5 $になったので、この値を$A×B$の2行2列目に代入します。
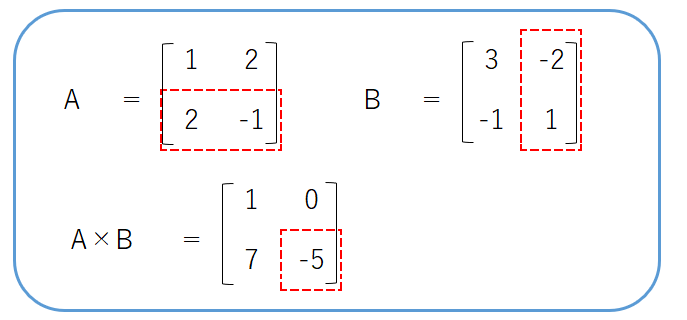
これで行列の計算が完了しました。
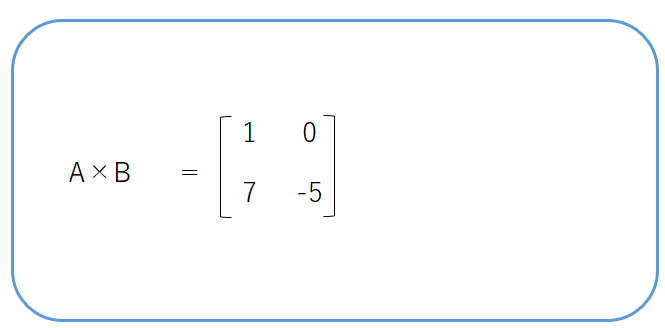
この行列の掛け算は3D数学の柱とも言えるほど、重要なものです。練習問題をしっかりと解いて、身につけましょう。
以下の行列の積 $A \times B$ を計算せよ。
| ① $A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$ | $B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}$ |
| ② $A = \begin{bmatrix} -1 & 0 \\ 2 & 3 \end{bmatrix}$ | $B = \begin{bmatrix} 4 & -2 \\ 1 & 5 \end{bmatrix}$ |
| ③ $A = \begin{bmatrix} 2 & -1 \\ 0 & 3 \end{bmatrix}$ | $B = \begin{bmatrix} -3 & 4 \\ 5 & 1 \end{bmatrix}$ |
| ④ $A = \begin{bmatrix} 6 & 2 \\ -1 & 4 \end{bmatrix}$ | $B = \begin{bmatrix} 0 & 3 \\ 5 & -2 \end{bmatrix}$ |
| ⑤ $A = \begin{bmatrix} 1 & -3 \\ 2 & 0 \end{bmatrix}$ | $B = \begin{bmatrix} -2 & 4 \\ 3 & 1 \end{bmatrix}$ |
