今までは行列同士の掛け算を学習しましたが、今回はベクトルと行列の掛け算を学びます。
ベクトルと行列の掛け算と言っても、特に特別な操作は必要なく、
ベクトルをただの2行1列の行列に変換して、行列の掛け算を実行するだけです。
行列とベクトルの掛け算の数式は以下になります。
行列 × ベクトルの定義(2×2 × 2×1の場合)
$ A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} $(2行2列の行列)
$ \vec{v} = (x,y) $(2次元ベクトル)
$ A\times\vec{v} = \begin{bmatrix}
a_{11}x + a_{12}y \\
a_{21}x + a_{22}y
\end{bmatrix} $(2次元ベクトル)
早速、以下の練習問題を計算してみましょう
練習
以下の行列とベクトルの積 $A\times \vec{v}$ を計算せよ。
$A = \begin{bmatrix} 2 & -1 \\ 1 & 3 \end{bmatrix},\quad \vec{v} = (4,\ 5)$
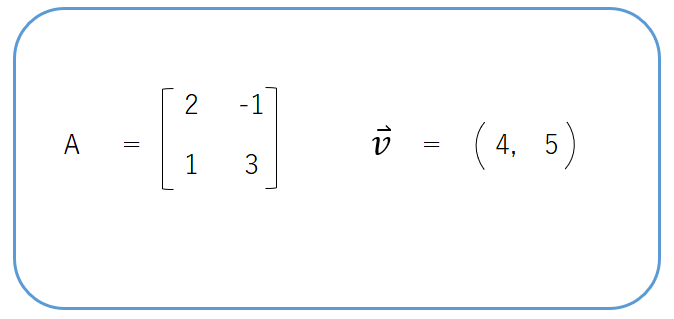
まず、ベクトルを2行1列に変換します。
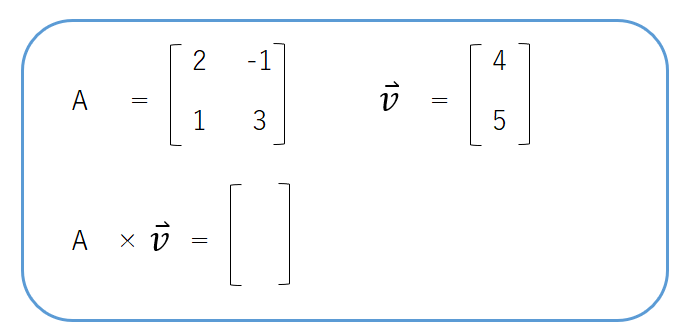
2行2列の行列と2行1列の行列の掛け算なので、掛け算後の行列の形は2行1列です。
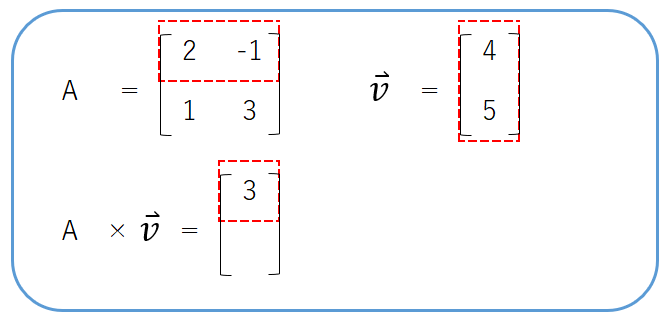
まずは、行列Aの1行目と、$\vec{v}$の1列目に対して、内積の計算を行います。
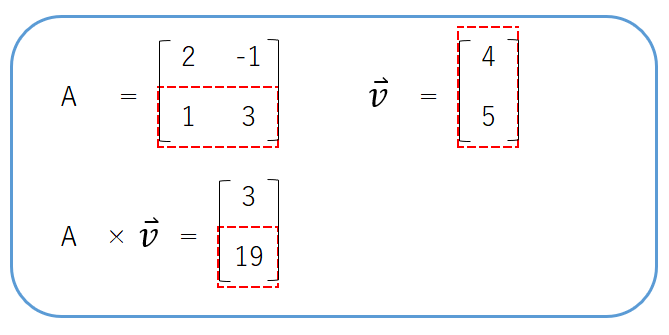
次に、行列Aの2行目と、$\vec{v}$の1列目に対して、内積の計算を行います。
最後に、計算結果をベクトルに変換したら、完了です。

これで行列の学習は一旦完了です。この行列とベクトルの掛け算は回転行列で使用する計算なので、しっかりと復習しておきましょう。
練習問題
以下の行列とベクトルの積 $A \vec{v}$ を計算せよ。
| ① $A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$ | $\vec{v} = (2,\ 1)$ |
| ② $A = \begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix}$ | $\vec{v} = (3,\ 4)$ |
| ③ $A = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}$ | $\vec{v} = (5,\ -3)$ |
| ④ $A = \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}$ | $\vec{v} = (-2,\ 7)$ |
| ⑤ $A = \begin{bmatrix} 3 & 1 \\ -2 & 4 \end{bmatrix}$ | $\vec{v} = (1,\ 2)$ |
