回転行列の原理

今までたくさんの事を学習してきましたが、全てこの回転行列に繋がっています。
回転行列とは以下の事です。

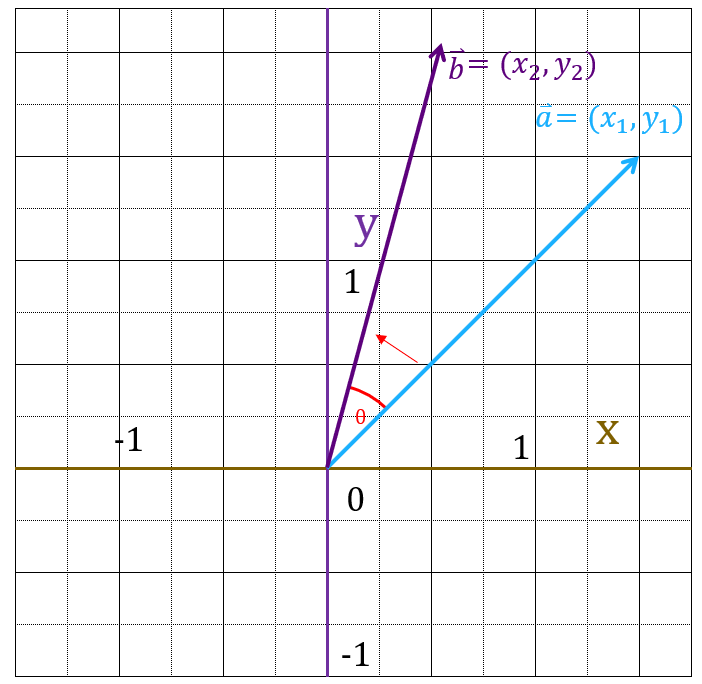
まず、x軸とベクトル$\vec{a}$の間の角度を$θ_1$とします。

もし、本当に、$\vec{b}$が、$\vec{a}$をθ回転させたベクトルであるならば、

$\vec{b}$を三角関数表示すると、以下になっているはずです。

$\vec{b}= (|\vec{a}|\times cos(\theta_1 + \theta),\; |\vec{a}|\times sin(\theta_1 + \theta)) $

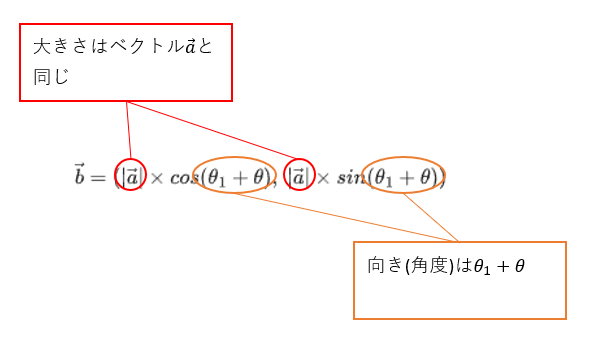
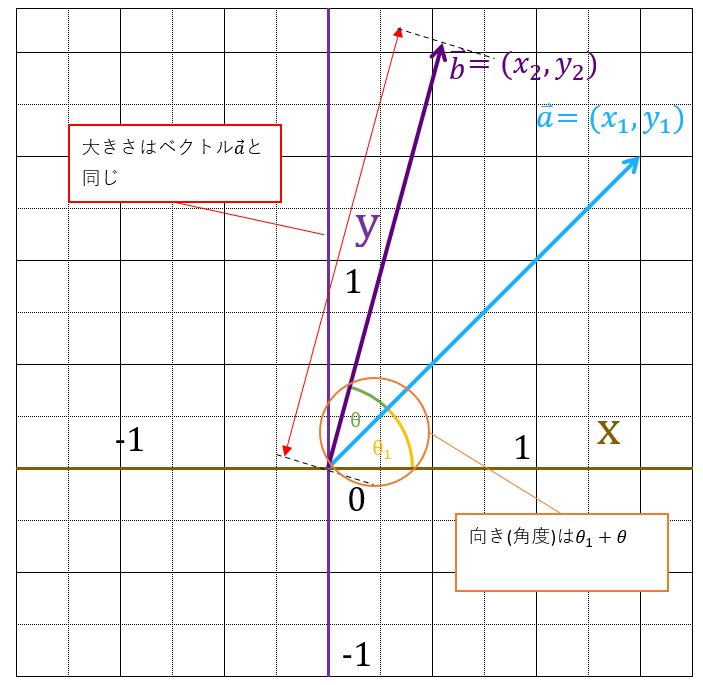
なので、実際に計算して、計算結果である$\boldsymbol{\vec{b}}$が、「$\boldsymbol{ (|\vec{a}|\times \cos(\theta_1 + \theta),\; |\vec{a}|\times \sin(\theta_1 + \theta))}$」となっていれば、$\boldsymbol{\vec{b}}$は、$\boldsymbol{\vec{a}}$をθ回転させたベクトルであると言えます。・・・・（１）

早速、実際に計算していきましょう。

まず、$\vec{a}$を事前に三角関数表示にしておきます。

$\vec{a}$を三角関数表示すると・・・

$\vec{a}= (x_1,\; y_1) = (|\vec{a}|\times cos\theta_1,\; |\vec{a}|\times sin\theta_1) $となります。

よって

$ \begin{bmatrix} x_1 \\ y_1 \end{bmatrix} = \begin{bmatrix} |\vec{a}|\times cos\theta_1 \\ |\vec{a}|\times sin\theta_1 \end{bmatrix} $

が成り立つので、

$ R(\theta)\times\vec{a} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \times \begin{bmatrix} x_1 \\ y_1 \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \times \begin{bmatrix} |\vec{a}|\times cos\theta_1 \\ |\vec{a}|\times sin\theta_1 \end{bmatrix} $

となります。

次に実際に計算してみます。

計算してみると、

$ \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \times \begin{bmatrix} |\vec{a}|\times\cos\theta_1 \\ |\vec{a}|\times\sin\theta_1 \end{bmatrix} = \begin{bmatrix} |\vec{a}|\times\cos\theta\cos\theta_1 – |\vec{a}|\times\sin\theta\sin\theta_1 \\ |\vec{a}|\times\sin\theta\cos\theta_1 + |\vec{a}|\times\cos\theta\sin\theta_1 \end{bmatrix} = \begin{bmatrix} |\vec{a}|\times(\cos\theta\cos\theta_1 – \sin\theta\sin\theta_1) \\ |\vec{a}|\times(\sin\theta\cos\theta_1 + \cos\theta\sin\theta_1) \end{bmatrix} $

になります。

ここで、この箇所に注目します。

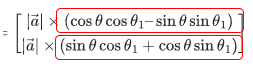
この箇所が、三角関数の加法定理の展開式になっています。

（加法定理についてはこちらのリンクを確認）

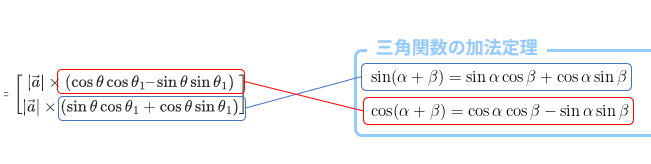
よって、加法定理より、以下が成り立ちます。

$ \begin{bmatrix} |\vec{a}|\times(\cos\theta\cos\theta_1 – \sin\theta\sin\theta_1) \\ |\vec{a}|\times(\sin\theta\cos\theta_1 + \cos\theta\sin\theta_1) \end{bmatrix} = \begin{bmatrix} |\vec{a}|\times\cos(\theta+\theta_1) \\ |\vec{a}|\times\sin(\theta+\theta_1) \end{bmatrix} $


最後に計算結果をベクトルに戻してやります
$ \begin{bmatrix} |\vec{a}|\times\cos(\theta+\theta_1) \\ |\vec{a}|\times\sin(\theta+\theta_1) \end{bmatrix} = (|\vec{a}|\times cos(\theta_1 + \theta),\; |\vec{a}|\times sin(\theta_1 + \theta)) $


この回転行列の計算によって得られたベクトル$\boldsymbol{\vec{b}=(|\vec{a}|\times cos(\theta_1 + \theta),\; |\vec{a}|\times sin(\theta_1 + \theta))}$は（１）と一致しています。

よって、回転行列の計算によって得られる$\vec{b}$

$ R(\theta)\times\vec{a} =\vec{b} $

は、$\vec{a}$をθ回転させたベクトルである。

証明終了