今回は回転行列を使って実際にベクトルを回転してみます。
練習
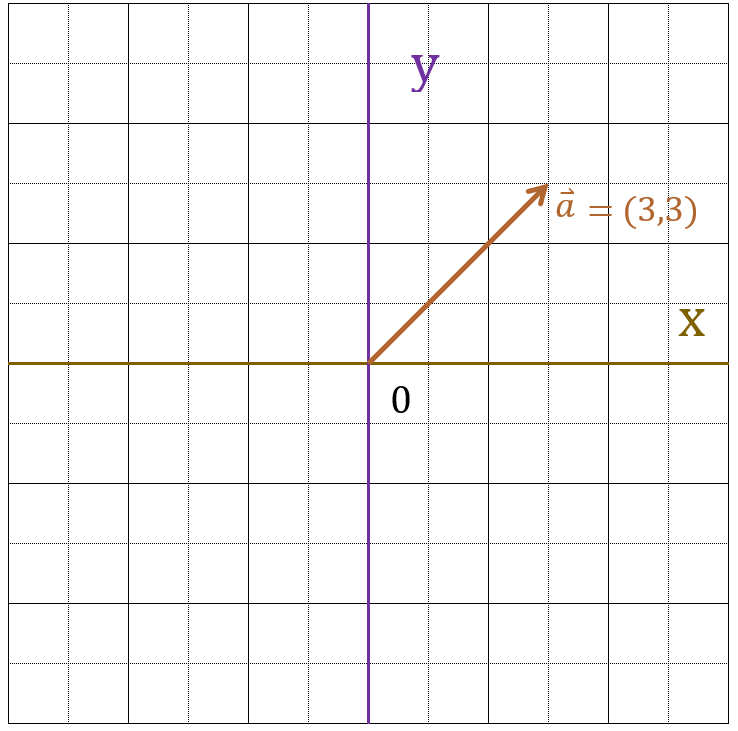
回転行列を使って、以下のベクトルを45度回転せよ
$\vec{a} = (3, 3) $
まず、回転行列を用意します。
回転行列
$ R(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} $
次に、三角関数表を使って、sinθ、とcosθを具体的な値に置き換えます。
$ \begin{bmatrix} \cos45^\circ & -\sin45^\circ \\ \sin45^\circ & \cos45^\circ \end{bmatrix} = \begin{bmatrix} 0.7071 & -0.7071 \\ 0.7071 & 0.7071 \end{bmatrix} $後は、この回転行列とベクトル$\vec{a}$を掛け算すれば回転が完了です。
$ R(45^\circ)\times\vec{a} = \begin{bmatrix} 0.7071 & -0.7071 \\ 0.7071 & 0.7071 \end{bmatrix} \begin{bmatrix} 3 \\ 3 \end{bmatrix} = \begin{bmatrix} 0.7071 \times 3 + (-0.7071) \times 3 \\ 0.7071 \times 3 + 0.7071 \times 3 \end{bmatrix} = \begin{bmatrix} 0 \\ 4.2426 \end{bmatrix} $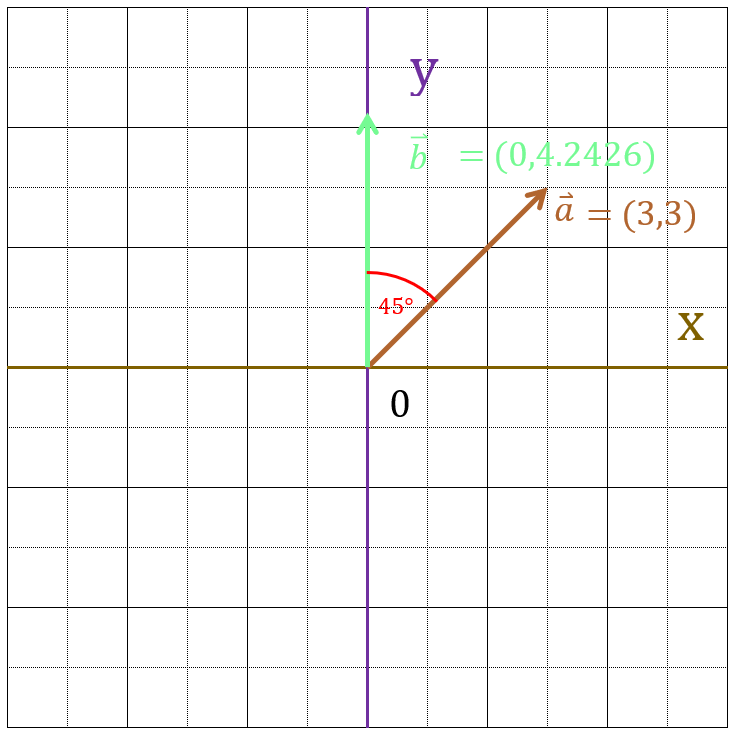
練習問題
以下のベクトルを回転行列を使用して指定の角度で回転せよ。
| ① $\vec{v} = (2,\ 2)$ | 角度:20° |
| ② $\vec{v} = (3,\ 15)$ | 角度:30° |
| ③ $\vec{v} = (-3,\ 3)$ | 角度:60° |
| ④ $\vec{v} = (5,\ -9)$ | 角度:90° |
| ⑤ $\vec{v} = (1,\ 0)$ | 角度:180° |
