今回は回転軸を指定して回転する方法を学びます。
回転行列は、原点(0,0)を回転軸にしており、原点を中心にしてのみしかベクトルを回転できません。
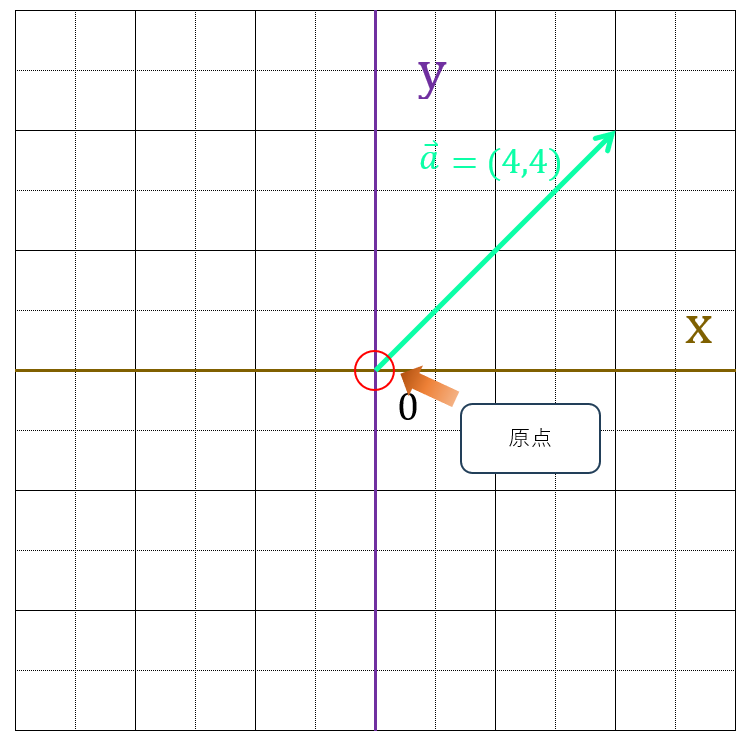
そのため、原点以外を回転軸にして回転させる場合は以下の操作が必要です。
回転軸を指定する操作
(1)回転軸ベクトルの逆ベクトルを、回転対象のベクトルに足す
(2)回転行列で回転を実行
(3)回転軸ベクトルを回転後のベクトルに足す
早速、$ \vec{a} = (4,4)$を、回転軸を(1, 3)にして45度回転してみましょう。
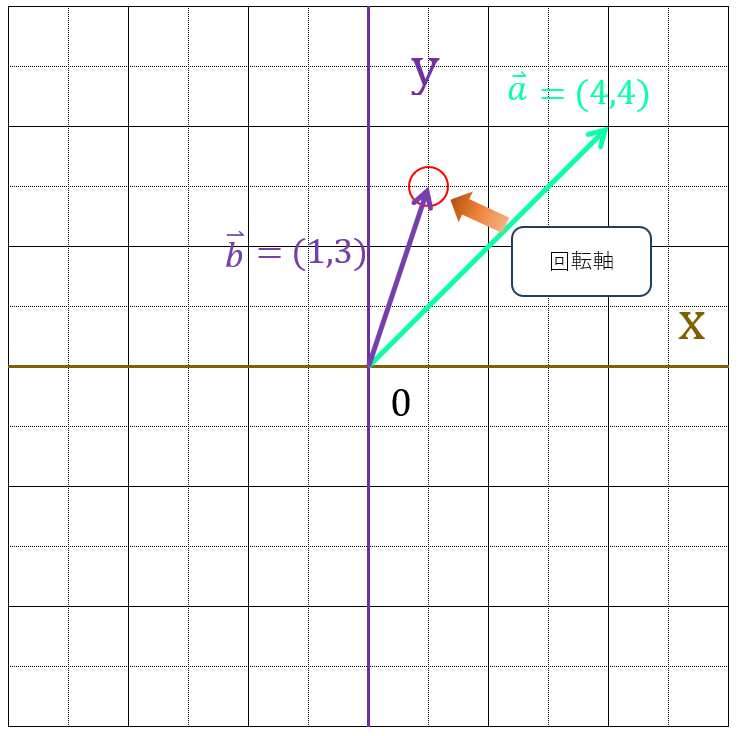
まず回転軸ベクトルと、回転対象のベクトルの両方に、回転軸ベクトルの逆ベクトル(逆向きのベクトル)を足します。
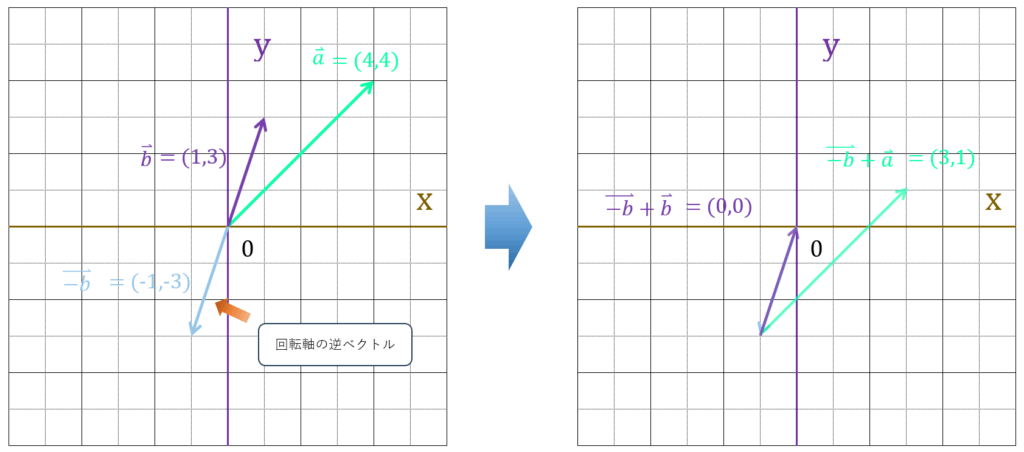
ここで、回転軸ベクトルを見てください。
回転軸ベクトルの逆ベクトルを足すことで、回転軸ベクトルの座標が原点に移動していることがわかります。
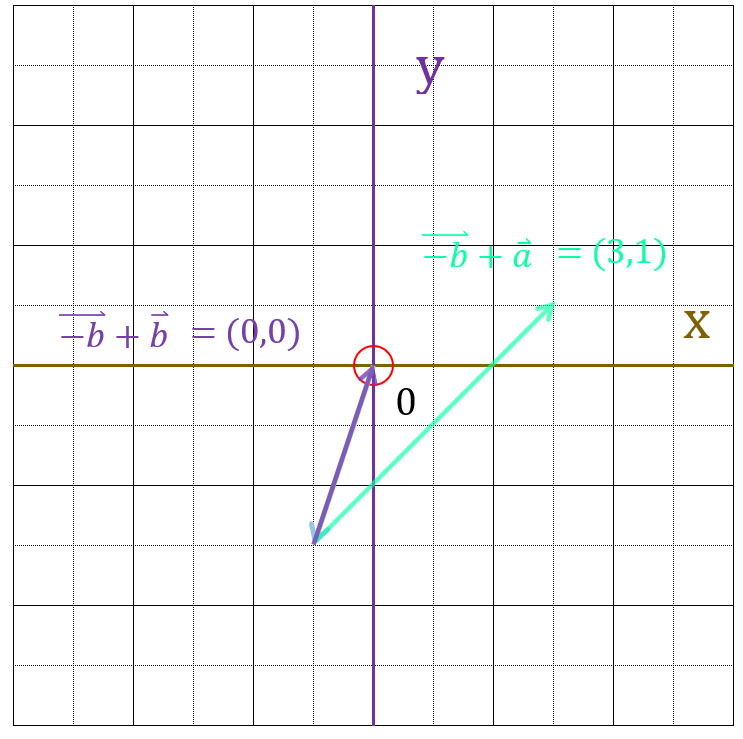
この状態で、回転行列を掛け算します。
$ R(45^\circ)\times(-\vec{b}+\vec{a}) = \vec{c} = \begin{bmatrix} 0.7071 & -0.7071 \\ 0.7071 & 0.7071 \end{bmatrix} \times \begin{bmatrix} 3 \\ 1 \end{bmatrix} = \begin{bmatrix} 0.7071 \cdot 3 + (-0.7071) \cdot 1 \\ 0.7071 \cdot 3 + 0.7071 \cdot 1 \end{bmatrix} = \begin{bmatrix} 1.4142 \\ 2.8284 \end{bmatrix} $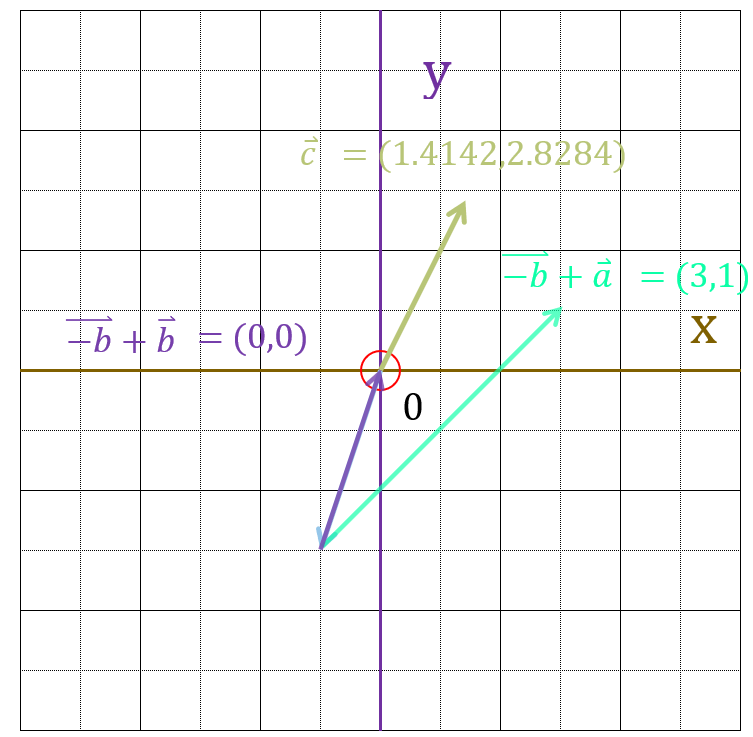
最後に、回転軸ベクトルを足して、位置を元に戻してやります。
これで、回転軸を指定した回転が完了です。
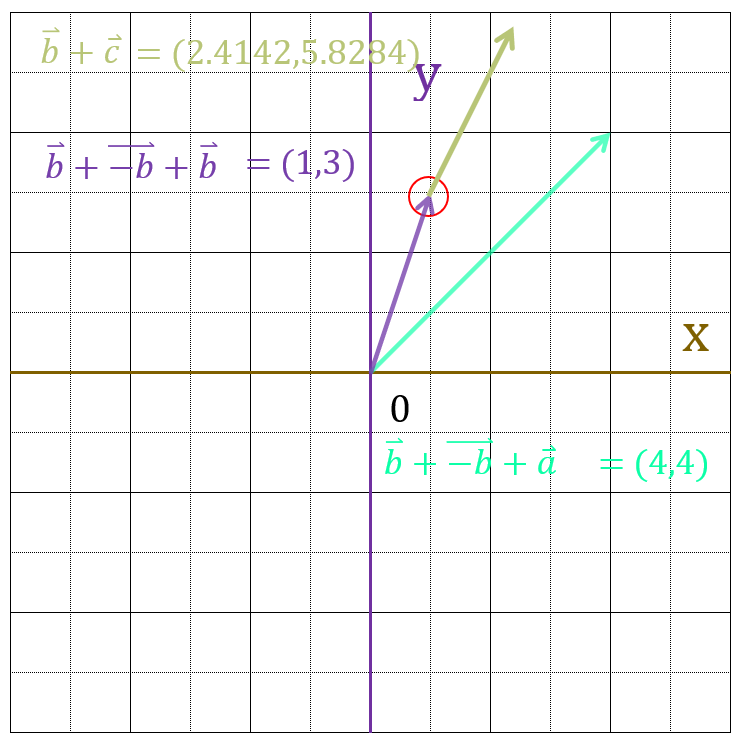
補助線を引くと、ちゃんと回転軸を中心にして45度回転しているのがわかります。
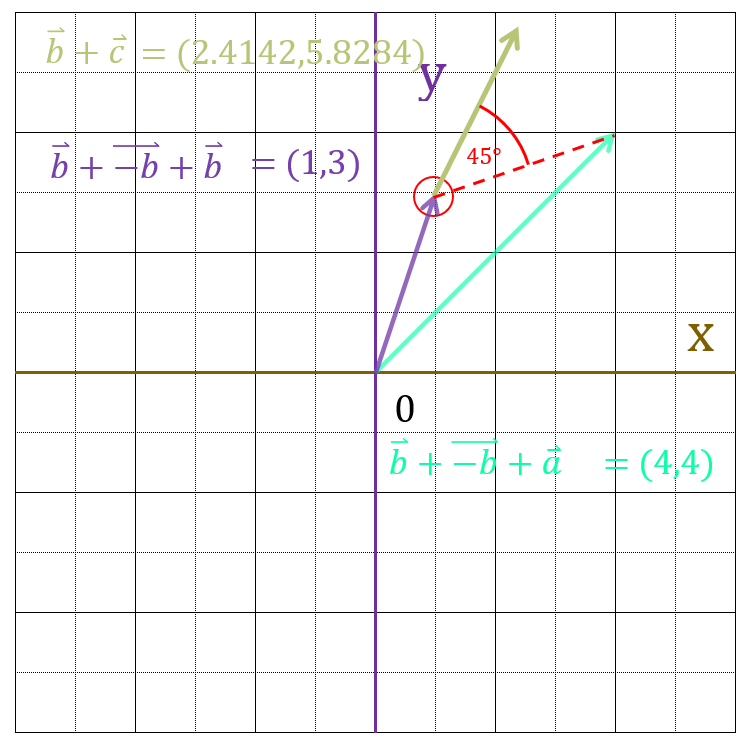
分度器を使って測ってみると、ちゃんと
45度ぴったり回転していることがわかります。
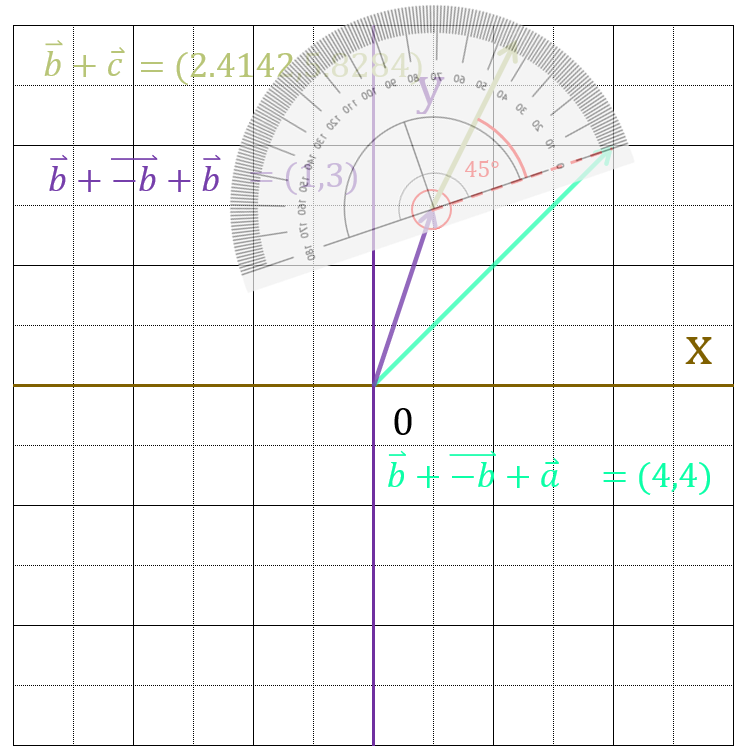
練習問題
以下のベクトルを回転行列を使用して指定の角度と、指定の回転軸で回転せよ。
| ① $\vec{v} = (2,\ 2)$ | 角度:45° | 回転軸:$(1,\ 1)$ |
| ② $\vec{v} = (3,\ -1)$ | 角度:90° | 回転軸:$(0,\ 1)$ |
| ③ $\vec{v} = (-2,\ 4)$ | 角度:30° | 回転軸:$(1,\ 0)$ |
| ④ $\vec{v} = (1,\ 0)$ | 角度:120° | 回転軸:$(\sqrt{3},\ 1)$ |
| ⑤ $\vec{v} = (-1,\ -1)$ | 角度:60° | 回転軸:$(-2,\ 1)$ |
