２つのベクトルのなす角度を求める

前回、ベクトルの内積を学びましたが、

ベクトルの内積を利用することで、２つのベクトルのなす角度を求めることができます。

ベクトルの内積の等式

$\vec{a} = (x_1, y_1)$

$\vec{b} = (x_2, y_2)$

$|\vec{a}|\times|\vec{b}|\times cos\theta = x_1 \cdot x_2 + y_1 \cdot y_2$

両辺を$ |\vec{a}|\times|\vec{b}| $で割って、以下の公式を得ることができます。

角度を求める公式

$cos\theta = \dfrac{x_1 \cdot x_2 + y_1 \cdot y_2}{|\vec{a}|\times|\vec{b}|}$

以下の２つのベクトルを例にして、実際に角度を求めてみましょう。

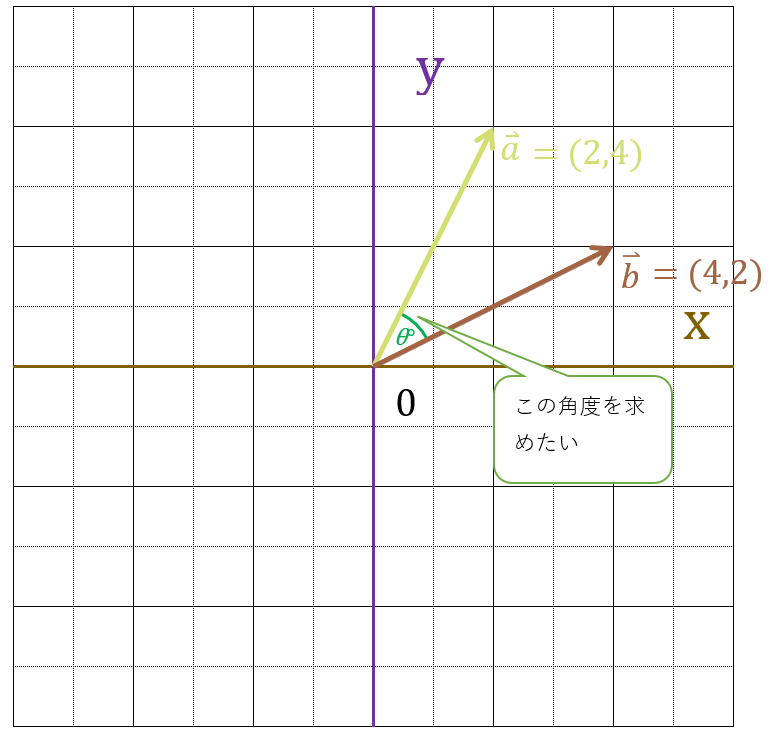
まずベクトルの大きさを求めます。

$|\vec{a}| = \sqrt{2^2 + 4^2} = \sqrt{20} = 2\sqrt{5}$

$|\vec{b}| = \sqrt{4^2 + 2^2} = \sqrt{20} = 2\sqrt{5}$

よって

$\cos\theta = \dfrac{x_1 \cdot x_2 + y_1 \cdot y_2}{|\vec{a}| \cdot |\vec{b}|} = \dfrac{2 \cdot 4 + 4 \cdot 2}{2\sqrt{5} \cdot 2\sqrt{5}} = \dfrac{16}{20} = \dfrac{4}{5}$

$\cos\theta = \dfrac{4}{5}$

これで、$ cos\theta $の値を求めることができました。

次は、この$ cos\theta $の値から、角度を特定します。

実は言うと、基本的にバチっと、$ cos\theta $の値から角度を求める公式は存在しません。

なので、実際に角度を求めたい場合は、三角関数の表を利用することになります。（三角関数の表へのリンクはこちら）

まず、$\dfrac{4}{5}$を分数ではなく小数に変更します。

$\dfrac{4}{5} = 0.8$

次に、三角関数表で、0.8に一番近い行を探します。

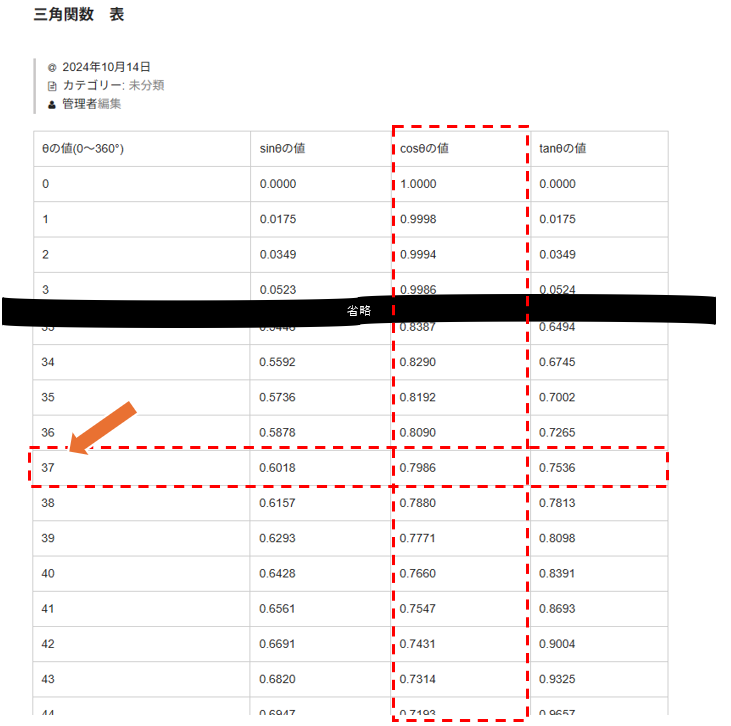
0.8に一番近いのは0.7986なので、さらにその行の一番左端の[θの値]列を確認してください。

「37」になっています。

これが、今回求めたいθの値( $cos\theta = 0.8$の時の、$\theta$の値）にります。

よって、$\vec{a} = (2,4)$と、$\vec{b} = (4,2)$のなす角度は37°です。

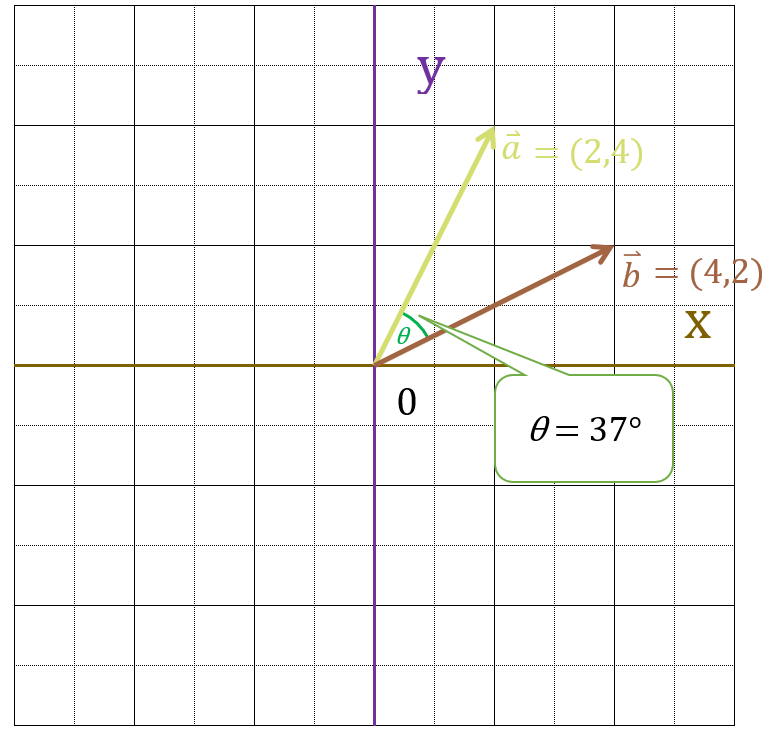
これで、ベクトルの学習は完了です。次は行列の学習に移ります。

解答はこちら

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル