三角関数は、$ sin\theta $、$ cos\theta $、$ tan\theta $のことです。
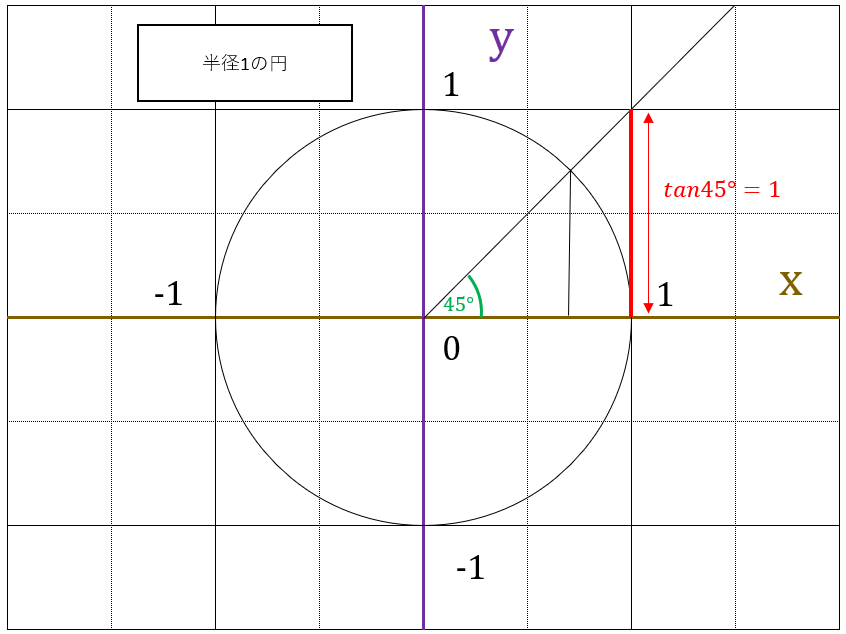
$ sin\theta $、$ cos\theta $は下記の図の位置の長さになります。
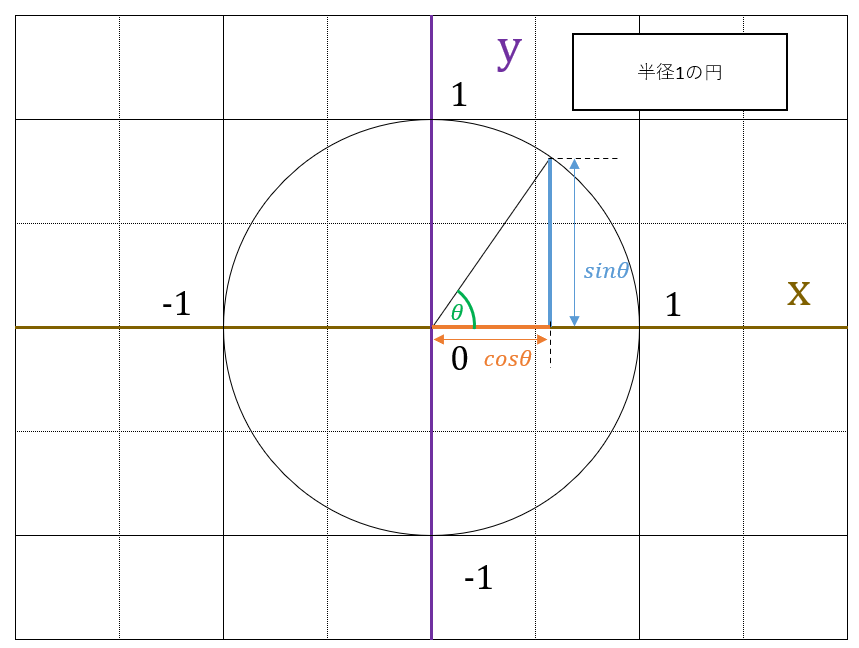
$ tan\theta $は、円とは関係なく、$ x=1 $ まで、線を延長したときの、下記の図の部分の長さになります。
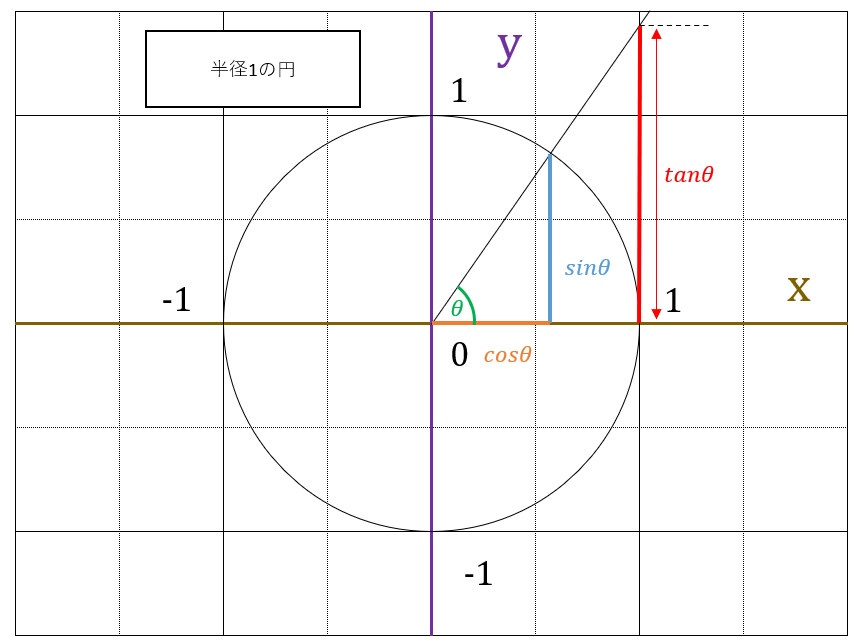
$ \theta = 45 $ であれば、$ sin45^\circ = \frac{\sqrt{2}}{2}, \quad cos45^\circ = \frac{\sqrt{2}}{2}, \quad tan45^\circ = 1 $となります。
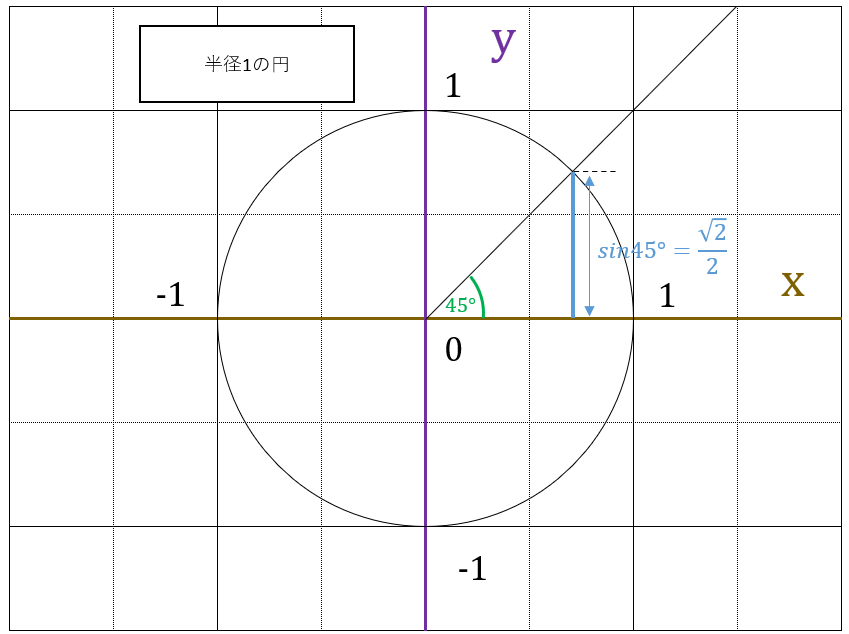
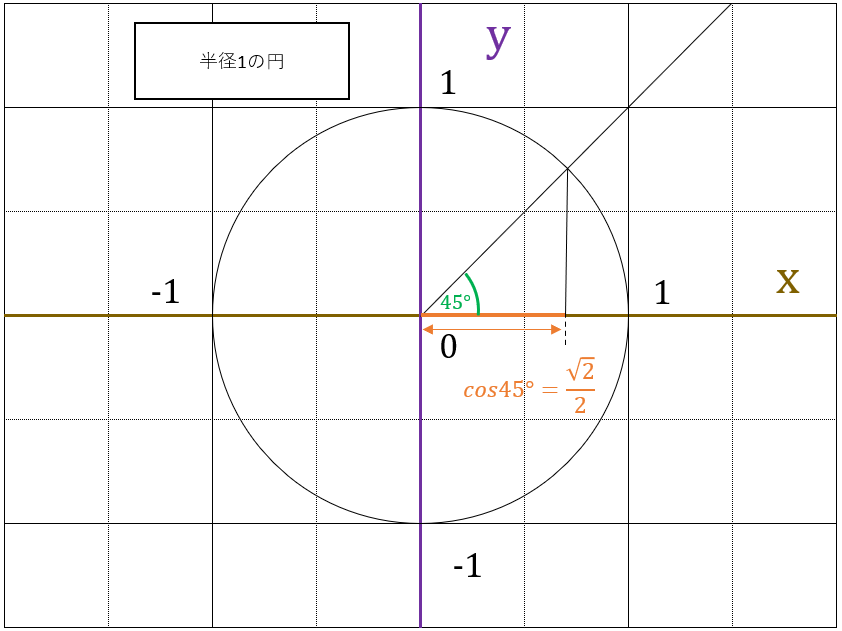
また、三角関数の値(例えば、sin27°など)を求める方法ですが、
バチっと角度だけ入れれば、三角関数の値を求めてくれる関数は存在しません。
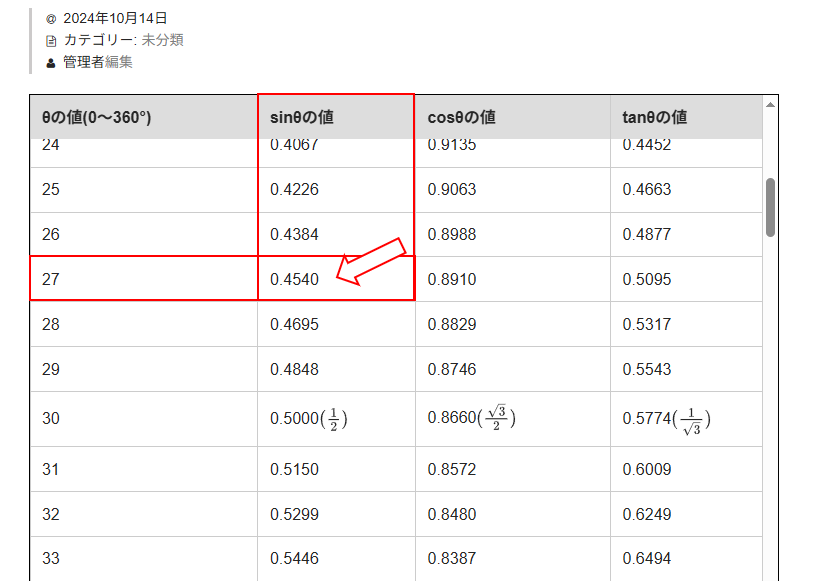
そのため、三角関数の値を求める時は、三角関数の表を使って求めます。
例えば、sin27°の値は、三角関数の表を使えば、「0.4540」であることがわかります。
練習問題
(問) 以下の値を求めよ。
① $ \cos27^\circ $
② $ \sin48^\circ $
③ $ \tan63^\circ $
④ $ \cos75^\circ $
⑤ $ \sin15^\circ $
