ベクトルの内積の定義は以下になります。
ベクトルの内積の定義
ポイント
【Q.】内積は何を表しているの?
【A.】内積は、特に何かを表しているかと言われると何も表していません。内積の式「$ \vec{a} \cdot \vec{b} = x_1 \cdot x_2 + y_1 \cdot y_2 $」単体では、何の役にも立ちません。しかし、この内積の式は後々解説する2つのベクトルのなす角を求めるときや、回転行列にも使用する非常に重要なものです。
また、ベクトルの内積は以下の等式が成りたちます。
ベクトルの内積の等式
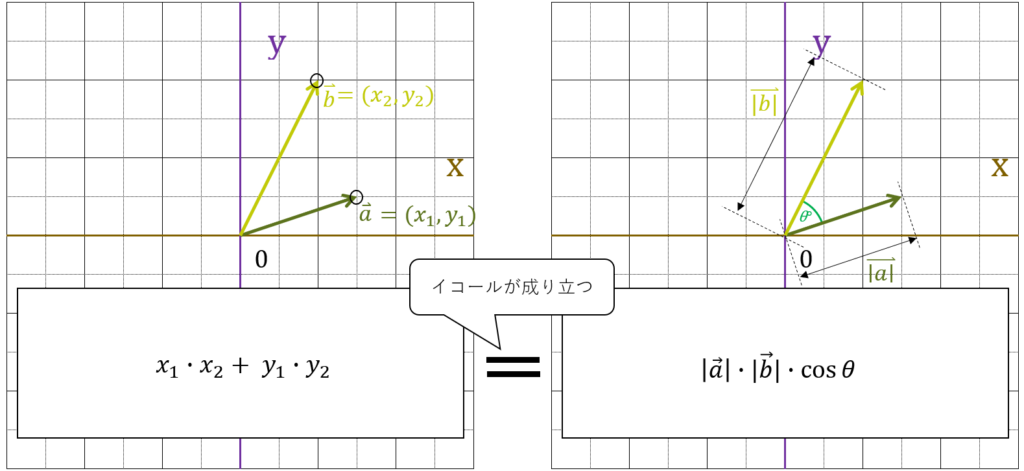
ポイント
【Q.】なぜ $ x_1 \cdot x_2 + y_1 \cdot y_2 = |\vec{a}|\times|\vec{b}|\times \cos\theta $ が成り立つの?
【A.】私も最初この等式を見たときに、本当に成り立つのか疑問を持ちました。そして、実際に証明してみたところ、確かに成り立ちます。しかし、証明をしようとすると、とても長くなるので、ここでは証明をはぶかせていただきます。
練習問題
(問1) 以下の内積を求めよ。
| ① $\vec{a} = (3,\ 3)$ | $\vec{b} = (4,\ 0)$ | |
| ② $\vec{a} = (2,\ -1)$ | $\vec{b} = (-1,\ 2)$ | |
| ③ $\vec{a} = (5,\ 0)$ | $\vec{b} = (0,\ 5)$ | |
| ④ $\vec{a} = (-3,\ 4)$ | $\vec{b} = (6,\ 8)$ | |
| ⑤ $\vec{a} = (1,\ 2)$ | $\vec{b} = (2,\ 1)$ |
(問2) 「問1」の各問題の内積を、「$ x_1 \cdot x_2 + y_1 \cdot y_2 $」と、「$|\vec{a}|\times|\vec{b}|\times \cos\theta $」の2つの公式を使ってそれぞれ求め、内積の値が一致することを確認せよ。
補足:2つのベクトルのなす角はそれぞれ以下である。
| ①:45° |
| ②:135° |
| ③:90° |
| ④:30° |
| ⑤:60° |
