ベクトルの大きさは、ベクトルの線の長さになります。
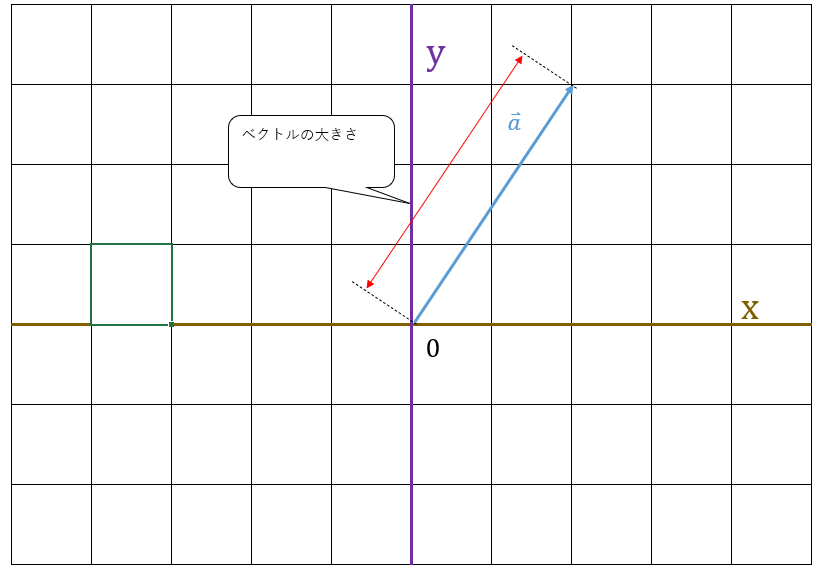
ベクトルの大きさを数式で書く場合、以下のようにベクトルを2つの線で囲って書きます。
ベクトルの大きさ
$ \vec{a} $の大きさ = $ |\vec{a}| $
ベクトルの大きさは、以下の数式で求めることができます。
ベクトルの大きさの公式
$ \vec{a} $ の座標を$ (x_1 , y_1) $ とすると$ \vec{a} $の大きさは
ベクトルの大きさの公式は、ピタゴラスの定理を使用することで求めることができます。
ベクトルの大きさの公式の証明
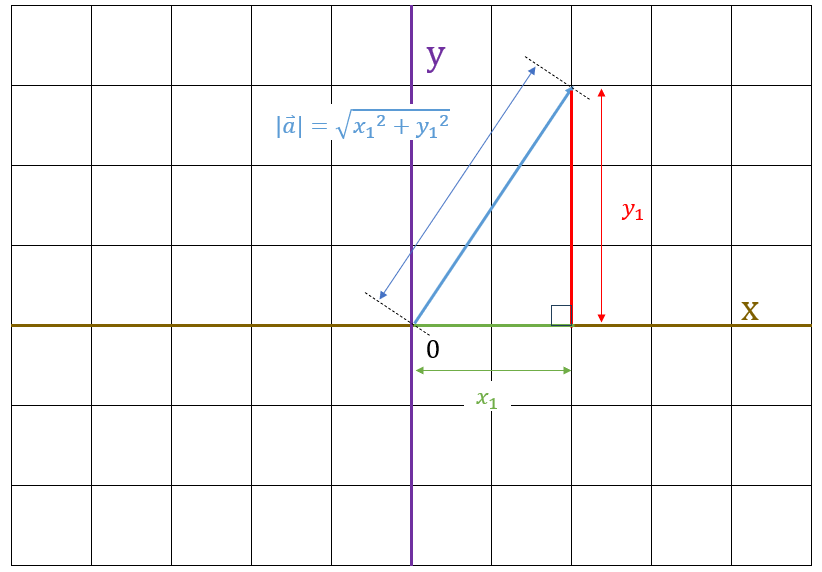
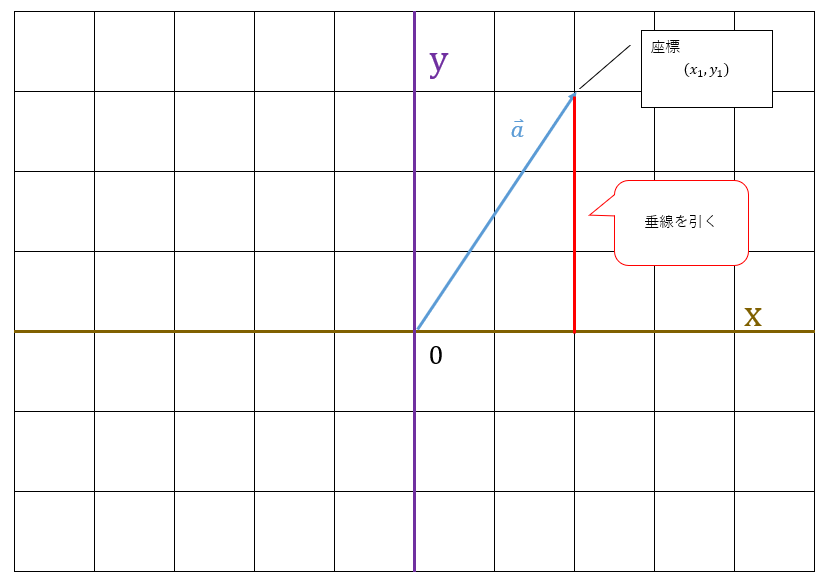
まず、ベクトルの座標から、X軸へと垂線を引きます。
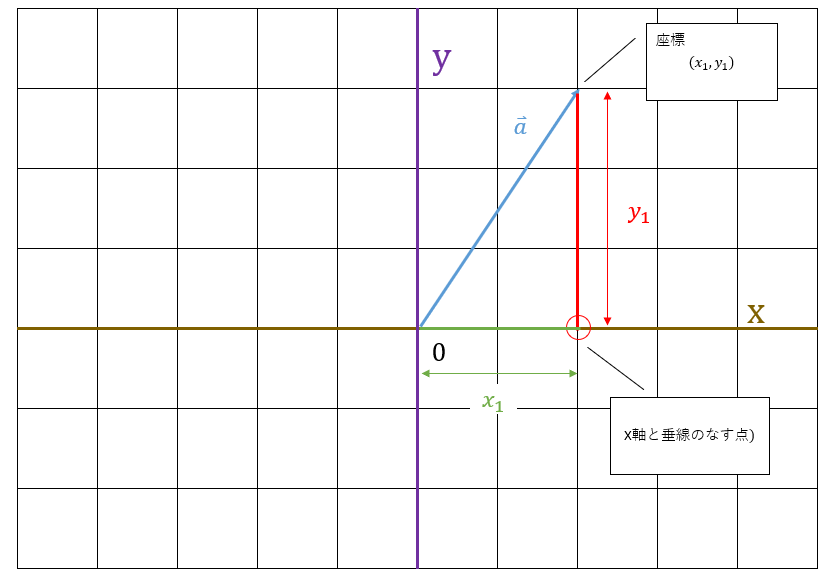
すると、原点から、X軸と垂線のなす点までの距離は $ x_1 $、X軸と垂線のなす点とベクトル$ \vec{a} $ までの距離は$ y_1 $となります。
さらに、垂線を引いたことで、直角三角形が作られたので、ピタゴラスの定理を適用できます。
ピタゴラスの定理を適用することでベクトル$ \vec{a} $の大きさを求めることができます。